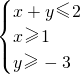练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知O为坐标原点，点A（1，-1），若点M（x，y）为平面区域 数学公式内的一个动点，则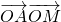数学公式的最大值与最小值之差为________．

    8
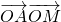    分析：根据向量数量积的坐标公式，得=x-y，目标函数z=x-y对应直线l，在直线l扫过区域的情况下将它进行平移，不难求出z的最大值为8，最小值为0，从而得到本题的答案．
    解答：解：作出不等式组 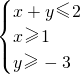对应的平面区域，如图中阴影部分三角形
    ∵点A（1，-1），M（x，y），
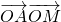    ∴=1×x+（-1）×y=x-y
    将直线l：z=x-y进行平移，可得当l经过点A（1，1）时，x-y有最小值0，
    当l经过点B（5，-3）时，x-y有最大值8，
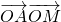    因此的最大值是8，最小值小值是0，它们的差是8
    故答案为：8
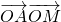    点评：本题给出平面区域内的两个点A、M，求数量积的最大值与最小值之差，着重考查了平面向量数量积的坐标运算和简单的线性规划等知识，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知O为坐标原点，点A（x，y）与点B关于x轴对称，
    j
    =(0，1)    ，则满足不等式
    OA
    2    +
    j
    •
    AB
    ≤0    的点A的集合用阴影表示（　　）
    A、精英家教网
    B、精英家教网
    C、精英家教网
    D、精英家教网

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知O为坐标原点，点A（2，1），点P在区域
    y≤x
    x+y≥2
    y＞3x-6
    内运动，则
    OA
    •
    OP
    的取值范围为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知O为坐标原点，点A（2，0），B（0，2），C（cosα，sinα），且0＜α＜π．
    （Ⅰ）若
    AC
    •
    BC
    =
    3
    5
    ，求tanα的值；
    （Ⅱ）若|
    OA
    +
    OC
    |=
    		7
    ，求
    OB
    与
    OC
    的夹角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•天河区三模）已知O为坐标原点，点M坐标为（-2，1），在平面区域
    x≥0
    x+y≤2
    y≥0
    上取一点N，则使|MN|为最小值时点N的坐标是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知O为坐标原点，点P（x，y），其中x，y满足
    x+2y-5≤0
    x+2y-3≥0
    x≥1
    y≥0
    ，则直线OP的斜率的最大值为
    2
    2
    ．

    查看答案和解析>>

    同步练习册答案