解:(1)∵
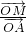
=

=
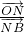
(2分)
∴
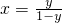
,从而
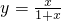
.(4分)
(2)当x∈[0,1]时,
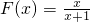
.
∵F(x)图象关于直线x=1对称,
∴F(2-x)=F(x),(5分)
∴F(x+2)=F(-x),又F(x)为偶函数,
∴F(x+2)=F(x).(7分)
设x∈[2k,2k+1],则x-2k∈[0,1],(8分)
∴
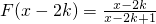
,即
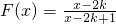
.(10分)
(3)不等式为
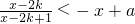
,(12分)
∴
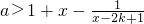
对x∈[2k,2k+1](k∈N)恒成立,
因此
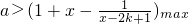
.(14分)
∵
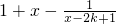
在x∈[2k,2k+1]上单调递增,
∴x=2k+1时其最大值为
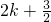
,
∴
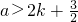
,即
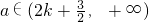
(k∈N).(16分)
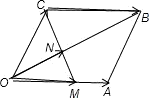
分析:(1)利用平行四边形对边平行且相等以及平行线分线段成比例可得x与y的关系.
(2)F(x)图象关于直线x=1对称?F(2-x)=F(x)?F(x+2)=F(-x)再利用F(x)=F(-x)可得F(x+2)=F(x).
在把x∈[2k,2k+1]转化为x-2k∈[0,1],利用x∈[0,1]时F(x)=f(x)可得x∈[2k,2k+1](k∈N)时的解析式.
(3)利用转化的思想把F(x)<-x+a转化为
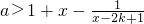
对x∈[2k,2k+1](k∈N)恒成立,再求后面的最大值即可.
点评:本题是对向量和函数的奇偶性,单调性,对称性和恒成立问题的综合考查,是一道综合性极强的好题.

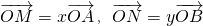 .
.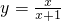 ;
;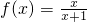 ,定义在R上的偶函数F(x),当x∈[0,1]时F(x)=f(x),且函数F(x)图象关于直线x=1对称,求证:F(x+2)=F(x),并求x∈[2k,2k+1](k∈N)时的解析式;
,定义在R上的偶函数F(x),当x∈[0,1]时F(x)=f(x),且函数F(x)图象关于直线x=1对称,求证:F(x+2)=F(x),并求x∈[2k,2k+1](k∈N)时的解析式; 解:(1)∵
解:(1)∵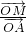 =
= =
=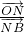 (2分)
(2分)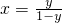 ,从而
,从而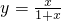 .(4分)
.(4分)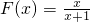 .
.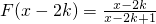 ,即
,即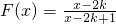 .(10分)
.(10分)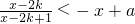 ,(12分)
,(12分)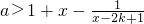 对x∈[2k,2k+1](k∈N)恒成立,
对x∈[2k,2k+1](k∈N)恒成立,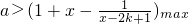 .(14分)
.(14分)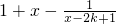 在x∈[2k,2k+1]上单调递增,
在x∈[2k,2k+1]上单调递增,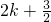 ,
,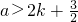 ,即
,即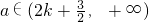 (k∈N).(16分)
(k∈N).(16分)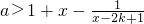 对x∈[2k,2k+1](k∈N)恒成立,再求后面的最大值即可.
对x∈[2k,2k+1](k∈N)恒成立,再求后面的最大值即可.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案 如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的动点.
如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的动点. 如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的动点.
如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的动点.