
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,方程
时,方程![]() 在区间
在区间![]() 内有唯一实数解,求实数
内有唯一实数解,求实数![]() 的取值范围;
的取值范围;
(2)对于区间![]() 上的任意不相等的实数
上的任意不相等的实数![]() 、
、![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:
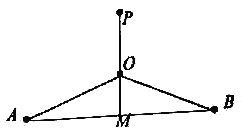
【题目】如图,已知![]() ,
,![]() 两个城镇相距20公里,设
两个城镇相距20公里,设![]() 是
是![]() 中点,在
中点,在![]() 的中垂线上有一高铁站
的中垂线上有一高铁站![]() ,
,![]() 的距离为10公里.为方便居民出行,在线段
的距离为10公里.为方便居民出行,在线段![]() 上任取一点
上任取一点![]() (点
(点![]() 与
与![]() ,
,![]() 不重合)建设交通枢纽,从高铁站铺设快速路到
不重合)建设交通枢纽,从高铁站铺设快速路到![]() 处,再铺设快速路分别到
处,再铺设快速路分别到![]() ,
,![]() 两处.因地质条件等各种因素,其中快速路
两处.因地质条件等各种因素,其中快速路![]() 造价为3百万元/公里,快速路
造价为3百万元/公里,快速路![]() 造价为2百万元/公里,快速路
造价为2百万元/公里,快速路![]() 造价为4百万元/公里, 设
造价为4百万元/公里, 设![]() ,总造价为
,总造价为![]() (单位:百万元).
(单位:百万元).
(1)求![]() 关于
关于![]() 的函数关系式,并指出函数的定义域;
的函数关系式,并指出函数的定义域;
(2)求总造价![]() 的最小值,并求出此时
的最小值,并求出此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
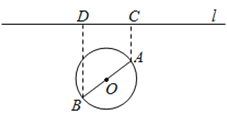
【题目】如图,一个湖的边界是圆心为![]() 的圆,湖的一侧有一条直线型公路
的圆,湖的一侧有一条直线型公路![]() ,湖上有桥
,湖上有桥![]() (
(![]() 是圆
是圆![]() 的直径).规划在公路
的直径).规划在公路![]() 上选两个点
上选两个点![]() ,并修建两段直线型道路
,并修建两段直线型道路![]() .规划要求:线段
.规划要求:线段![]() 上的所有点到点
上的所有点到点![]() 的距离均不小于圆
的距离均不小于圆![]() 的半径.已知点
的半径.已知点![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() 和
和![]() (
(![]() 为垂足),测得
为垂足),测得![]() ,
,![]() ,
,![]() (单位:百米).
(单位:百米).
(1)若道路![]() 与桥
与桥![]() 垂直,求道路
垂直,求道路![]() 的长;
的长;
(2)在规划要求下,![]() 和
和![]() 中能否有一个点选在
中能否有一个点选在![]() 处?并说明理由.
处?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在锐角△ABC中,∠BAC≠60°,过点B、C分别作△ABC外接圆的切线BD、CE,且满足![]() ,直线DE与AB、AC的延长线分别交于点F、G、CF与BD交于点M,CE与BG交于点N.证明:
,直线DE与AB、AC的延长线分别交于点F、G、CF与BD交于点M,CE与BG交于点N.证明:![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某地有三家工厂,分别位于矩形ABCD的顶点A,B以及CD的中点P处,已知AB=20km,CB=10km,为了处理三家工厂的污水,现要在矩形ABCD内(含边界),且与A,B等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为![]() km.
km.

(I)设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
(II)确定污水处理厂的位置,使三条排污管道的总长度最短,并求出最短值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P—ABCD中,PA⊥平面ABCD,∠DAB=∠ADC=90°,DC=![]() AB,F,M分别是线段PC,PB的中点.
AB,F,M分别是线段PC,PB的中点.

(1)在线段AB上找出一点N,使得平面CMN∥平面PAD,并给出证明过程;
(2)若PA=![]() AB,DC=
AB,DC=![]() AD,求二面角C—AF—D的余弦值.
AD,求二面角C—AF—D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com