
����Ŀ����ͼ��ij�������ҹ������ֱ�λ�ھ���ABCD�Ķ���A��B�Լ�CD���е�P������֪AB=20km��CB=10km��Ϊ�˴������ҹ�������ˮ����Ҫ�ھ���ABCD��(���߽�)������A��B�Ⱦ����һ��O������һ����ˮ�����������������۹ܵ�AO��BO��OP�������۹ܵ����ܳ�Ϊ![]() km��
km��

(I)��![]() ����
����![]() ��ʾ��
��ʾ��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
(II)ȷ����ˮ��������λ�ã�ʹ�������۹ܵ����ܳ�����̣���������ֵ��
���𰸡���I��![]() ��II����ˮ��������λ��Ϊ��Pλ���߶�AB���д������Ҿ���
��II����ˮ��������λ��Ϊ��Pλ���߶�AB���д������Ҿ���![]() ����
����![]()
��������
(I)��ֱ��������AOQ��,����AQ=10,![]() �������OA��OQ,�Ӷ��ɵ�OP=10-OQ,
�������OA��OQ,�Ӷ��ɵ�OP=10-OQ,
Ȼ��ɵ�![]() ,��д��
,��д��![]() �ķ�Χ,���ɵõ�.
�ķ�Χ,���ɵõ�.
(II)���õ����õ������ĵ�����,���ݵ����Կ���ú�������ֵ.
��I��������PQ��ֱƽ��AB����![]() ����
����![]() ��
��
��![]() ��
��![]() ,����
,����![]() ,
,
����![]() ��
��
��������ϵʽΪ![]()
��II��![]() ,
,
��![]() ,��
,��![]() ,
,![]() ,����
,����![]() ,
,
��![]() ʱ,
ʱ,![]() ,
,![]() ��
��![]() �ļ�����,
�ļ�����,
��![]() ʱ,
ʱ,![]() ,
, ![]() ��
��![]() ��������,
��������,
���Ե�![]() ʱ,
ʱ,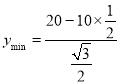
![]() ,
,
��ʱ��![]() λ���߶�
λ���߶�![]() ���д�����,�Ҿ���
���д�����,�Ҿ���![]() ��
��![]()
![]() ��.
��.
�����������۹ܹܵ��ܳ����Ϊ![]()


 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P����������8km��A������������1km��B������һ����������Ĺ�·AC��BD���ּƻ���AC��BD·�߸���һ����������E��F��Ϊ���⽻ͨѹ�����������������ഹֱ�Ĺ�·PE��PF�����EPA=����0������ ![]() ����
���� 
��1��Ϊ���ٶ��ܱ������Ӱ�죬��ȷ��E��F��λ�ã�ʹ��PAE���PFB�����֮����С��
��2��Ϊ��ʡ����ɱ�����ȷ��E��F��λ�ã�ʹPE+PF��ֵ��С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˶�Ա�������ѵ������֪���ǻ��еĻ������ȶ���7��8��9��10������ÿ������ɼ�����Ӱ�죮���������Ƶ�ʷֲ�����ͼ���£�
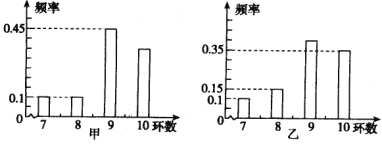
����Ƶ����Ϊ���ʣ��ش��������⣺
(1)����˶�Ա��3�������������1�λ���9������(��9��)�ĸ��ʣ�
(2)���ס������˶�Ա�������1�Σ�![]() ��ʾ��2������л���9������(��9��)�Ĵ�������
��ʾ��2������л���9������(��9��)�Ĵ�������![]() �ķֲ��м�����
�ķֲ��м�����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵΪ�˽�����ij���ŶԱ���ҵְ���ķ���������������50��ְ����������50��ְ���Ըò��ŵ����֣�����Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ���������������ݷ�������Ϊ![]()

��1����Ƶ�ʷֲ�ֱ��ͼ��![]() ��ֵ��
��ֵ��
��2�����Ƹ���ҵ��ְ���Ըò������ֲ�����80�ĸ��ʣ�
��3����������![]() ���ܷ�ְ���У������ȡ2�ˣ����2�����ֶ���
���ܷ�ְ���У������ȡ2�ˣ����2�����ֶ���![]() �ĸ���.
�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ģ�ij��ͬѧ���ù���ڽ������ʵ������![]() �����Ⱥ�����ȡ
�����Ⱥ�����ȡ![]() �˽�����һ������ϰ���Ƿ���ϵ�̼����ĵ��飬������ϰ�߷��ϵ�̼����ij�Ϊ����̼�塱�������Ϊ���ǵ�̼�塱���õ�����ͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��
�˽�����һ������ϰ���Ƿ���ϵ�̼����ĵ��飬������ϰ�߷��ϵ�̼����ij�Ϊ����̼�塱�������Ϊ���ǵ�̼�塱���õ�����ͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��


��1����ȫƵ�ʷֲ�ֱ��ͼ����![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
��2����![]() ������εġ���̼�塱�в��÷ֲ��������ȡ
������εġ���̼�塱�в��÷ֲ��������ȡ![]() �˲μӻ����̼����������ѡȡ
�˲μӻ����̼����������ѡȡ![]() ����Ϊ��ӣ���ѡȡ��
����Ϊ��ӣ���ѡȡ��![]() �������������
�������������![]() �������Ϊ
�������Ϊ![]() ����
����![]() �ķֲ��к�����
�ķֲ��к�����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ҫ�õ�����f��x��=2sinxcosx��x��R��ͼ��ֻ�轫����g��x��=2cos2x��1��x��R��ͼ�� ��
A.����ƽ�� ![]() ����λ
����λ
B.����ƽ�� ![]() ����λ
����λ
C.����ƽ�� ![]() ����λ
����λ
D.����ƽ�� ![]() ����λ
����λ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ʯ��ׯ��ij��������˾�ҵ���һ������Ա�Ĺ������ù�˾������������нн�귽������������н100Ԫ��ÿ����һ������1Ԫ���ҷ�������н140Ԫ��ÿ��ǰ55��û�н���������55���IJ���ÿ������12Ԫ��
������ֱ�����ס�������н�귽������нy����λ��Ԫ�����ͻ�����n�ĺ�����ϵʽ��
�����ݸù�˾��������Ա100������ͼ�¼����������Ա����ƽ�����͵���������������������100���е�������ָ��������ͼ��ʾ��ֱ��ͼ�����е�ij���������ָ���ڣ�![]() ��
��![]() ]��n��1��2��3��4��5��ʱ����ƽ��������Ϊ50��2n��������Ƶ����Ϊ���ʣ��ش��������⣺
]��n��1��2��3��4��5��ʱ����ƽ��������Ϊ50��2n��������Ƶ����Ϊ���ʣ��ش��������⣺

�ٸ����������ݣ���ÿ������Ա����нΪX����λ��Ԫ�����Էֱ�����ס������ַ�������нX�ķֲ��У���ѧ���������
�ڽ�Ϣ��е����ݣ�����ͳ��ѧ��˼�룬����С����������ѡ������н�귽���ȽϺ��ʣ���˵��������ɡ�
���ο����ݣ�0��62��0��36��1��42��1��9 6��2��6 2��6��76��3��42��1 1��56��3��62��12��96��4��62��21��16��15��62��243��36��20��42��416��16��44��42��1971��36��
���𰸡������������ĺ�����ϵʽΪ�� ![]() ���ҷ����ĺ�����ϵʽΪ��
���ҷ����ĺ�����ϵʽΪ��![]() �������ټ��������ڼ�����.
�������ټ��������ڼ�����.
��������
������������ɵü���������Ա��н![]() ����λ��Ԫ�����͵���
����λ��Ԫ�����͵���![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ�� ![]() �� �ҷ���������Ա��н
�� �ҷ���������Ա��н![]() ����λ��Ԫ�����͵���
����λ��Ԫ�����͵���![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��![]() .
.
�����������������X�ķֲ��У��ݴ˼���ɵ�![]() ��
��![]() ��
��![]() .
.
�ڴ�һ�������ϵļ����֪��![]() ԶС��
ԶС��![]() ���������չ������벨����Խ�С������С��Ӧѡ�����.
���������չ������벨����Խ�С������С��Ӧѡ�����.
�𰸶��������ϵļ��������Կ�����![]() ������С��Ӧѡ���ҷ���.
������С��Ӧѡ���ҷ���.
������������Ա��н![]() ����λ��Ԫ�����͵���
����λ��Ԫ�����͵���![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ�� ![]() ��
��
�ҷ���������Ա��н![]() ����λ��Ԫ�����͵���
����λ��Ԫ�����͵���![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��![]()
������������֪������100���У��ù�˾����Ա��ƽ�����͵����������±���
���� | 52 | 54 | 56 | 58 | 60 |
Ƶ�� | 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
����![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 152 | 154 | 156 | 158 | 160 |
| 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
����![]()
����![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 140 | 152 | 176 | 200 |
| 0.5 | 0.2 | 0.2 | 0.1 |
����![]()
![]()
�ڴ�һ�������ϵļ����֪����Ȼ![]() ��������������
��������������![]() ԶС��
ԶС��![]() ���������չ������벨����Խ�С������С��Ӧѡ�����.
���������չ������벨����Խ�С������С��Ӧѡ�����.
�𰸶��������ϵļ��������Կ�����![]() ���������չ�������С���ҷ����չ�������������С��Ӧѡ���ҷ���.
���������չ�������С���ҷ����չ�������������С��Ӧѡ���ҷ���.
���㾦��
������Ҫ����Ƶ�ʷֲ�ֱ��ͼ����ѧ�����뷽��ĺ�����ʵ��Ӧ�õ�֪ʶ�����ڿ���ѧ����ת�������ͼ����������.
�����͡������
��������
20
����Ŀ����֪��ԲC��![]() ��a��b��0�������ҽ���ֱ�ΪF1��F2����������Ϊ
��a��b��0�������ҽ���ֱ�ΪF1��F2����������Ϊ![]() ��MΪ��Բ������һ�㣬����F1MF2��90��ʱ����F1MF2�����Ϊ1��
��MΪ��Բ������һ�㣬����F1MF2��90��ʱ����F1MF2�����Ϊ1��
��������ԲC�ķ��̣�
������֪��A����ԲC��������Բ�����һ�㣬�ӳ�ֱ��AF1��AF2�ֱ�����Բ���ڵ�B��D����ֱ��BD��б��Ϊk1��ֱ��OA��б��Ϊk2����֤��k1��k2���ڶ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ֱ������ϵ��ԭ���غϣ�������x����������غϣ�ԲC�ļ����귽���Ǧ�=asin�ȣ�ֱ��l�IJ��������� 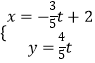 ��tΪ������
��t������
��1����a=2��ֱ��l��x��Ľ�����M��N��ԲC��һ���㣬��|MN|�����ֵ��
��2��ֱ��l��ԲC�صõ��ҳ�����ԲC�İ뾶�� ![]() ������a��ֵ��
������a��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com