已知抛物线y=ax2+bx在第一象限内与直线x+y=4相切.此抛物线与x轴所围成的图形的面积记为S.求使S达到最大值的a,b值,并求S的最大值.
解:依题设可知抛物线与x轴的交点的横坐标分别为x
1=0,
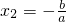
,
所以
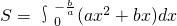
=(
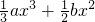
)
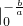
=
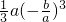
+
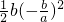
=
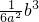
(1)…(4分)
又直线x+y=4与抛物线y=ax
2+bx相切,
即它们有唯一的公共点
由方程组
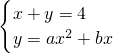
,
得ax
2+(b+1)x-4=0,其判别式△必须为0,
即△=(b+1)
2+16a=0,
于是
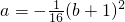
,…(8分)
代入(1)式得:
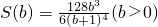
,
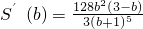
.
令S′(b)=0,在b>0时,得b=3;
当0<b<3时,S′(b)>0;
当b>3时,S′(b)<0.
故在b=3时,S(b)取得极大值,也是最大值,
即a=-1,b=3时,S取得最大值,且
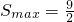
.…(12分)
分析:依题设可知抛物线与x轴的交点的横坐标分别为x
1=0,
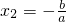
,所以
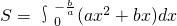
=
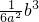
.由直线x+y=4与抛物线y=ax
2+bx相切,知ax
2+(b+1)x-4=0中△=(b+1)
2+16a=0,由此能求出S达到最大值的a,b值及S的最大值.
点评:本题考查抛物线和直线的综合运用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意定积分的合理运用.

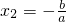 ,
,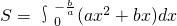 =(
=(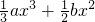 )
)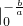
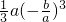 +
+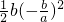
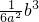 (1)…(4分)
(1)…(4分)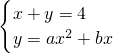 ,
,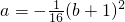 ,…(8分)
,…(8分)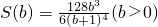 ,
,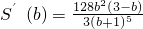 .
.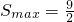 .…(12分)
.…(12分)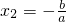 ,所以
,所以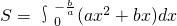 =
=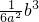 .由直线x+y=4与抛物线y=ax2+bx相切,知ax2+(b+1)x-4=0中△=(b+1)2+16a=0,由此能求出S达到最大值的a,b值及S的最大值.
.由直线x+y=4与抛物线y=ax2+bx相切,知ax2+(b+1)x-4=0中△=(b+1)2+16a=0,由此能求出S达到最大值的a,b值及S的最大值.

 全优点练单元计划系列答案
全优点练单元计划系列答案