
| A. | $\frac{kπ}{2}+\frac{π}{4}$ | B. | $\frac{kπ}{2}$ | C. | kπ+$\frac{π}{4}$ | D. | kπ-$\frac{π}{4}$(其中k∈Z) |
分析 根据方程关系进行化简,结合三角函数的性质进行求解即可.
解答 解:∵f(x)=e${\;}^{2{x}^{2}-1}$,
∴若f[cos($\frac{π}{2}$+θ)]=1,
则f(-sinθ)=1,
即${e}^{2si{n}^{2}θ-1}$=1,
即2sin2θ-1=0,
则2sin2θ=1,
sin2θ=$\frac{1}{2}$,
即sinθ=±$\frac{\sqrt{2}}{2}$,
即θ=2kπ+$\frac{π}{4}$或2kπ-$\frac{π}{4}$或θ=2kπ+π++$\frac{π}{4}$或2kπ-π-$\frac{π}{4}$
即θ=$\frac{kπ}{2}$+$\frac{π}{4}$,
故选:A.
点评 本题主要考查函数值的求解,利用三角函数的性质进行化简是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
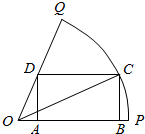 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的运动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的运动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∪B=B | B. | A∩B=A | C. | A∪(CUB)=U | D. | (CUA)∪B=U |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 数列中不能重复出现同一个数 | |
| B. | 1,2,3,4与4,3,2,1是同一数列 | |
| C. | 1,1,1,1…不是数列 | |
| D. | 两个数列的每一项相同,则数列相同 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com