
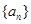 中,公差d >0,
中,公差d >0,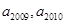 是方程
是方程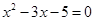 的两个根,
的两个根,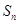 是数列
是数列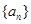 的前n项的和,那么满足条件
的前n项的和,那么满足条件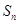 >0的最小自然数n=( )
>0的最小自然数n=( )| A.4018 | B.4017 | C.2009 | D.2010 |
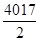 ×(a2009+a2010)=3×2009>0, S(2009×2-1)=S4017=
×(a2009+a2010)=3×2009>0, S(2009×2-1)=S4017=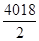 (a2009+a2009)=a2009×4017<0,所以Sn>0的最大n=4018.故选A.
(a2009+a2009)=a2009×4017<0,所以Sn>0的最大n=4018.故选A.

科目:高中数学 来源:不详 题型:填空题
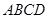 的面积为1,把它的各边延长一倍得到新正方形
的面积为1,把它的各边延长一倍得到新正方形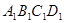 ,再把正方形
,再把正方形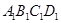 的各边延长一倍得到正方形
的各边延长一倍得到正方形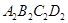 (如图2),如此进行下去,正方形
(如图2),如此进行下去,正方形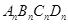 的面积为 .(用含有
的面积为 .(用含有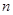 的式子表示,
的式子表示,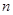 为正整数)
为正整数)
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
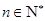 ,数列
,数列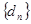 满足
满足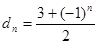 ,数列
,数列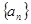 满足
满足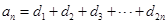 ;数列
;数列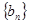 为公比大于
为公比大于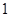 的等比数列,且
的等比数列,且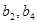 为方程
为方程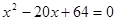 的两个不相等的实根.
的两个不相等的实根.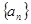 和数列
和数列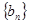 的通项公式;
的通项公式;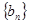 中的第
中的第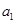 项,第
项,第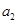 项,第
项,第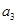 项,……,第
项,……,第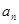 项,……删去后剩余的项按从小到大的顺序排成新数列
项,……删去后剩余的项按从小到大的顺序排成新数列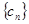 ,求数列
,求数列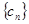 的前
的前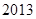 项和.
项和.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com