
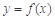 满足:当
满足:当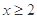 时,
时,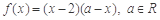 ,当
,当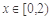 时,
时,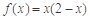 .
.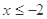 时,
时,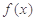 的表达式;
的表达式;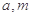 满足什么条件时,函数
满足什么条件时,函数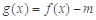 有4个零点,且这4个零点从小到大依次构成等差数列.
有4个零点,且这4个零点从小到大依次构成等差数列.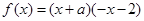 ;(2)①
;(2)①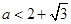 时,
时,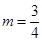 ;②
;②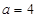 时,
时,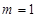 ;③
;③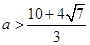 时,
时,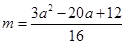 .
.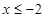 转化成
转化成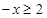 ,利用已知
,利用已知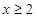 时的解析式,利用偶函数转化解析式;第二问,把
时的解析式,利用偶函数转化解析式;第二问,把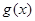 有4个零点,先转化为
有4个零点,先转化为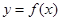 与
与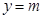 有4个交点且均匀分布,所以利用等差中项,偶函数等基础知识列出表达式,分情况进行讨论分析.
有4个交点且均匀分布,所以利用等差中项,偶函数等基础知识列出表达式,分情况进行讨论分析.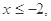 则
则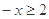 ,
,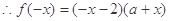 ,
, 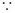
 偶函数
偶函数 ,
,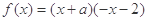 .
.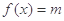 零点
零点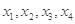 ,
,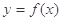 与
与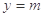 交点有4个且均匀分布,
交点有4个且均匀分布,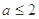 时,
时, 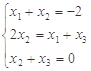 得
得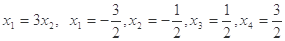 ,
, 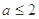 时,
时,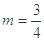 ,
, 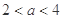 且
且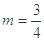 时 ,
时 ,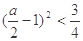 ,
, 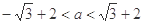 ,
,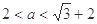 时,
时,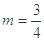 ,
,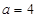 时
时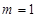 时,符合题意,
时,符合题意,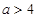 时,
时,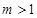 ,
,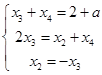 ,
,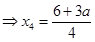 ,
,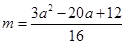 ,
,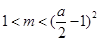 ,所以
,所以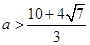 或
或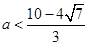 (舍)
(舍)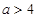 且
且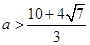 时,
时,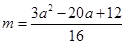 时存在.
时存在.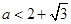 时,
时,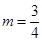 ;
;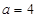 时,
时,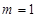 ;
;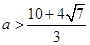 时,
时,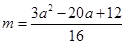 符合题意.
符合题意.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源:不详 题型:解答题
 是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛
是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛 扩建成一个更大的矩形花园
扩建成一个更大的矩形花园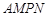 ,要求:B在
,要求:B在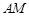 上,D在
上,D在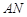 上,对角线
上,对角线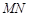 过C点,且矩形
过C点,且矩形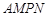 的面积小于64平方米.
的面积小于64平方米.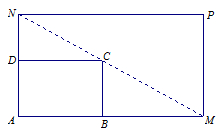
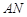 长为
长为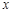 米,矩形
米,矩形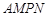 的面积为
的面积为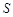 平方米,试用解析式将
平方米,试用解析式将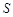 表示成
表示成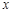 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;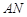 的长度是多少时,矩形
的长度是多少时,矩形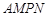 的面积最小?并求最小面积.
的面积最小?并求最小面积.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
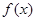 的定义域为
的定义域为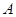 ,若存在非零实数
,若存在非零实数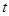 ,使得对于任意
,使得对于任意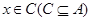 有
有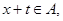 且
且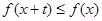 ,则称
,则称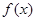 为
为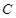 上的
上的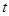 度低调函数.已知定义域为
度低调函数.已知定义域为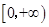 的函数
的函数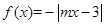 ,且
,且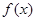 为
为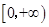 上的
上的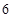 度低调函数,那么实数
度低调函数,那么实数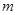 的取值范围是( )
的取值范围是( )A.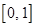 | B.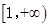 | C.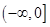 | D.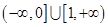 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com