练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知A，B都是锐角，且A+B≠
    π
    2
    ，（1+tanA）（1+tanB）=2，求证：A+B=
    π
    4
    ．
    考点：两角和与差的正切函数
    专题：三角函数的图像与性质
    分析：直接利用两角和的正切函数，化简已知条件，求出A+B的正切，然后得到结果．
    解答： 证明：1+tanA+tanB+tanAtanB=2，
    ∴1-tanAtanB=tanA+tanB，
    又∵A+B≠
    π
    2

    ∴1-tanAtanB≠0
    ∴
    tanA+tanB
    1-tanAtanB
    =1
    ∴tan（A+B）=1
    又∵A，B是锐角
    ∴A+B=
    π
    4
    ．
    点评：本题考查两角和与差的三角函数，角的范围以及公式的灵活运用的解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    下列命题：①?x∈C，x2≥0；②?x∈R，x2≥x；③7≥7；④“x2≠1”的充要条件是“x≠1或x≠-1”，其中真命题的个数是（　　）
    A、0B、1C、2D、3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    等差数列{an}中，若a3=5，a5=3，则a1+a7=（　　）
    A、4B、8C、-4D、-8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知二次函数f（x）=ax2+bx（a≠0），f（2）=0且方程f（x）=x有两个相等的实数根．
    （1）求f（x）的解析式；
    （2）求f（x）的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    袋中装有m个红球和n个白球（m≥n≥2），这些红球和白球除了颜色不同之外，其余都相同，从袋中同时取出2个球，
    （1）若取出的两个球都是红球的概率是取出的两个球是1红1白的概率的整数倍，试证：m必为奇数．
    （2）若取出的球是同色球的概率等于取出不同色球的概率，试求适合m+n≤40的所有数组（m，n）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    有5名学生站成一排照相，
    （1）甲、乙两人必须相邻，有几种排法？
    （2）甲、乙两人不相邻，有几种排法？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在关于人体脂肪含量y（百分比）和年龄x关系的研究中，得到如下一组数据
    年龄x232739414550
    脂肪含量y9.517.821.225.927.528.2
    （Ⅰ）画出散点图，判断x与y是否具有相关关系；
    （Ⅱ）通过计算可知
    b
    =0.6512，
    a
    =-2.72，请写出y对x的回归直线方程，并计算出23岁和50岁的残差．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知α、β∈（0，π），且tanα、tanβ是方程x2-3x-5=0的两根．
    （1）求tan（α+β）的值；
    （2）求cos（2α+2β）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

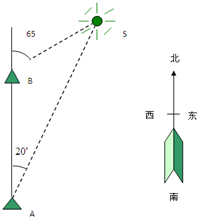    如图，一艘船以32.2n mile/h的速度向正北航行．在A处看灯塔S在船的北偏东20°的方向，30min后航行到B处，在B处看灯塔在船的北偏东65°的方向，已知距离此灯塔6.5n mile以外的海区为航行安全区域，这艘船可以继续沿正北方向航行吗？

    查看答案和解析>>

    同步练习册答案