已知函数y=f(x)是定义在(0,+∞)上的函数,有f(2)=1,对于任意的x>0,y>0,都有f(xy)=f(x)+f(y),且满足当x>1时,f(x)>0成立.
(1)求f(1)、f(4)的值;
(2)求满足f(x)+f(x-3)>2的x的取值范围.
解:(1)令x=y=1,则f(1)=f(1)+f(1),∴f(1)=0.
令x=y=2,则f(2×2)=f(2)+f(2),∴f(4)=2f(2)=2×1=2.
(2)下面先证明函数f(x)在区间(0,+∞)上是增函数.
证明:任取x
1,x
2满足0<x
1<x
2,则

,由已知得
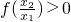
.
∴f(x
2)=
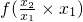
=
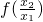
+f(x
1)>f(x
1),即f(x
2)>f(x
1),
∴函数f(x)在区间(0,+∞)是单调递增.
∵f(x)+f(x-3)=f(x
2-3x)>2=f(4),∴x
2-3x>4,解得x>4,或x<-1,
而已知x>0,∴x<-1应舍去,
故x的取值范围是x>4.
分析:(1)分别令x=y=1,及x=y=2,即可求出函数值f(1),f(4).
(2)先利用已知条件证明此函数的单调性,进而利用单调性把自变量解放出来,从而求出x的取值范围.
点评:本题考查了抽象函数的求值及利用其单调性求自变量的取值范围,充分理解抽象函数的条件和恰当的取值是解题的关键.

 ,由已知得
,由已知得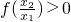 .
.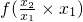 =
=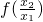 +f(x1)>f(x1),即f(x2)>f(x1),
+f(x1)>f(x1),即f(x2)>f(x1),

 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为