
 ,任取
,任取 ,记函数
,记函数 在区间
在区间 上的最大值为
上的最大值为 最小值为
最小值为 记
记 . 则关于函数
. 则关于函数 有如下结论:
有如下结论: 为偶函数;
为偶函数;  的值域为
的值域为 ;
; 的周期为2;
的周期为2; 的单调增区间为
的单调增区间为 .
. ,其中
,其中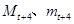 分别是指函数
分别是指函数 在区间
在区间 上的最大值、最小值,注意到函数
上的最大值、最小值,注意到函数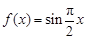 是最小正周期为
是最小正周期为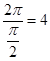 的函数,所以
的函数,所以 在区间
在区间 的图像与在
的图像与在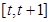 的图像完全相同,所以
的图像完全相同,所以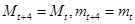 ,所以
,所以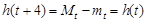 ,所以函数
,所以函数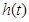 的一个周期为4,对该函数性质的研究,只须先探究
的一个周期为4,对该函数性质的研究,只须先探究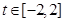 的性质即可.
的性质即可.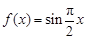 的图像(如下图(1))与性质可知
的图像(如下图(1))与性质可知
 时,
时, 在区间
在区间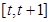 的最小值为
的最小值为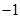 ,最大值为
,最大值为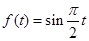 ,此时
,此时
 时,
时, 在区间
在区间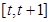 的最小值为
的最小值为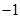 ,最大值为
,最大值为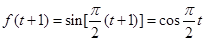 ,此时
,此时 ;
;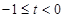 时,
时, 在区间
在区间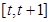 的最小值为
的最小值为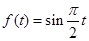 ,最大值为
,最大值为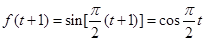 ,此时
,此时 ;
;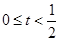 时,
时, 在区间
在区间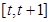 的最小值为
的最小值为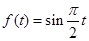 ,最大值为1,此时
,最大值为1,此时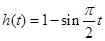 ;
;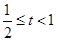 时,
时, 在区间
在区间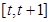 的最小值为
的最小值为 ,最大值为1,此时
,最大值为1,此时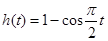 ;
;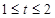 时,
时, 在区间
在区间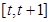 的最小值为
的最小值为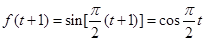 ,最大值为
,最大值为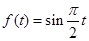 ,此时
,此时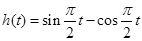
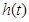 的图像,如下图(2)所示
的图像,如下图(2)所示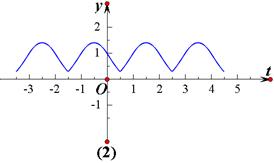
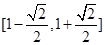 ,从图中可以看到函数的最小正周期为2,函数的单调递增区间为
,从图中可以看到函数的最小正周期为2,函数的单调递增区间为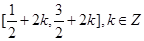 ,故只有③④正确.
,故只有③④正确.

科目:高中数学 来源:不详 题型:解答题
 处取得最大值2,其图象与x轴的相邻两个交点的距离为
处取得最大值2,其图象与x轴的相邻两个交点的距离为 .
. 的值域.
的值域.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .
. 的单调递减区间;
的单调递减区间; 的图像向左平移
的图像向左平移 个单位,再将所得图像上各点的横坐标缩短为原来的
个单位,再将所得图像上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数 的图像,求
的图像,求 在
在 上的值域.
上的值域.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .
. 在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);
在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);

 的单调递增区间;
的单调递增区间; 时,求函数
时,求函数 的最大值和最小值及相应的
的最大值和最小值及相应的 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com