
已知函数f(x)=ex-e-x(x∈R且e为自然对数的底数).
(1)判断函数f(x)的奇偶性与单调性;
(2)是否存在实数t,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立?若存在,求出t;若不存在,请说明理由.
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练x4-1练习卷(解析版) 题型:填空题
如图,点D在⊙O的弦AB上移动,AB=4,连接OD,过点D作OD的垂线交⊙O于点C,则CD的最大值为________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练4练习卷(解析版) 题型:填空题
已知函数f(x)=aln x+x在区间[2,3]上单调递增,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练3练习卷(解析版) 题型:选择题
已知a>0,b>0,且2a+b=4,则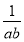 的最小值为( ).
的最小值为( ).
A.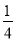 B.4 C.
B.4 C.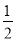 D.2
D.2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练2练习卷(解析版) 题型:选择题
若函数y=f(x)(x∈R)满足f(x+1)=-f(x),且x∈[-1,1]时f(x)=1-x2.函数g(x)= 则函数h(x)=f(x)-g(x)在区间[-5,4]内的零点的个数( ).
则函数h(x)=f(x)-g(x)在区间[-5,4]内的零点的个数( ).
A.7 B.8?,
C.9 D.10
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(解析版) 题型:填空题
已知f(x)=ln(1+x)的定义域为集合M,g(x)=2x+1的值域为集合N,则M∩N=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习7-2随机变量及其分布练习卷(解析版) 题型:解答题
以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
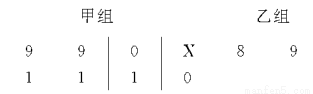
(1)如果X=8,求乙组同学植树棵数的平均数和方差;
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y的分布列和数学期望.(注:方差s2=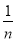 [(x1-
[(x1-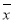 )2+(x2-
)2+(x2-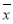 )2+…+(xn-
)2+…+(xn- )2],其中
)2],其中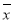 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-2椭圆、双曲线、抛物线练习卷(解析版) 题型:选择题
已知直线l过抛物线C的焦点,且与C的对称轴垂直,l与C交于A、B两点,|AB|=12,P为C的准线上一点,则△ABP的面积为( ).
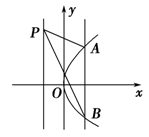
A.18 B.24 C.36 D.48
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习4-1等差数列与等比数列练习卷(解析版) 题型:解答题
设数列{an}的前n项和为Sn,已知ban-2n=(b-1)Sn.
(1)证明:当b=2时,{an-n·2n-1}是等比数列;
(2)求{an}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com