设数列{an}的前n项和为Sn，已知ban－2n＝(b－1)Sn.
(1)证明：当b＝2时，{an－n·2n－1}是等比数列；
(2)求{an}的通项公式．
（1）见解析（2）an＝
【解析】由题意知a1＝2，且ban－2n＝(b－1)Sn，ban＋1－2n＋1＝(b－1)Sn＋1，
两式相减得b(an＋1－an)－2n＝(b－1)an＋1，
即an＋1＝ban＋2n.①
(1)证明 当b＝2时，由①知an＋1＝2an＋2n，
于是an＋1－(n＋1)·2n＝2an＋2n－(n＋1)·2n＝2(an－n·2n－1)，
又a1－1·21－1＝1≠0，所以{an－n·2n－1}是首项为1，公比为2的等比数列．
(2)当b＝2时，由(1)知an－n·2n－1＝2n－1，即an＝(n＋1)·2n－1；当b≠2时，由①得，an＋1－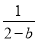
·2n＋1＝ban＋2n－
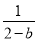·2n＋1＝ban－
·2n＝b 
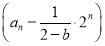，因此an＋1－
·2n＋1＝b 
＝
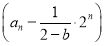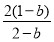·bn，
得an＝
科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练1练习卷（解析版） 题型：解答题
已知函数f(x)＝ex－e－x(x∈R且e为自然对数的底数)．
(1)判断函数f(x)的奇偶性与单调性；
(2)是否存在实数t，使不等式f(x－t)＋f(x2－t2)≥0对一切x都成立？若存在，求出t；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习5-2空间向量与立体几何练习卷（解析版） 题型：解答题
如图所示的长方体ABCD-A1B1C1D1中，底面ABCD是边长为2的正方形，O为AC与BD的交点，BB1＝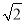
，M是线段B1D1的中点．
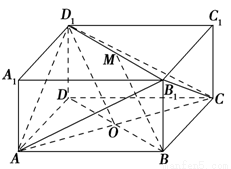
(1)求证：BM∥平面D1AC；
(2)求证：D1O⊥平面AB1C；
(3)求二面角B-AB1-C的大小．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习5-1空间几何体与点等练习卷（解析版） 题型：选择题
若某多面体的三视图(单位：cm)如图所示，则此多面体的体积是( )．
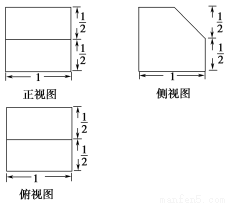
A.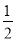
cm3 B.
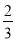cm3 C. 
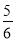cm3 D. 
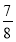cm3
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习4-2数列求和与数列的综合应用练习卷（解析版） 题型：选择题
等比数列{an}的前n项和公式Sn，若2S4＝S5＋S6，则数列{an}的公比q的值为 ( )．
A．－2或1 B．－1或 2 C．－2 D．1
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习4-1等差数列与等比数列练习卷（解析版） 题型：选择题
已知等比数列{an}中，a1＝1，且4a2,2a3，a4成等差数列，则a2＋a3＋a4等于 ( )．
A．1 B．4 C．14 D．15
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习3-2解三角形练习卷（解析版） 题型：填空题
在△ABC中，a，b，c分别为角A，B，C的对边，已知a、b、c成等比数列，且a2－c2＝ac－bc，则A＝________，△ABC的形状为________．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习3-1三角函数与三角恒等变换练习卷（解析版） 题型：选择题
已知函数y＝sin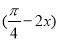
，则下列结论中正确的是( )．
A．关于点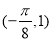
中心对称
B．关于直线x＝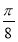
轴对称
C．向左平移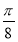
后得到奇函数
D．向左平移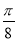
后得到偶函数
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练选修4-4练习卷（解析版） 题型：解答题
在直角坐标系xOy中，椭圆C的参数方程为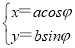
(φ为参数，a>b>0)，在极坐标系(与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴)中，直线l与圆O的极坐标方程分别为ρsin(θ＋
)＝
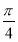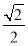m(m为非零数)与ρ＝b.若直线l经过椭圆C的焦点，且与圆O相切，求椭圆C的离心率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com