
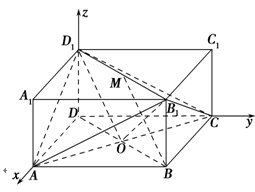
如图所示的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,O为AC与BD的交点,BB1=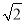 ,M是线段B1D1的中点.
,M是线段B1D1的中点.
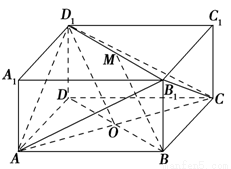
(1)求证:BM∥平面D1AC;
(2)求证:D1O⊥平面AB1C;
(3)求二面角B-AB1-C的大小.
60°.
【解析】(1)证明 建立如图所示的空间直角坐标系,则点O(1,1,0)、D1(0,0,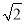 ),
),
∴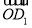 =(-1,-1,
=(-1,-1,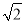 ),
),
又点B(2,2,0),M(1,1, ),
),
∴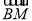 =(-1,-1,
=(-1,-1,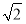 ),
),
∴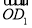 =
= ,又∵OD1与BM不共线,
,又∵OD1与BM不共线,
∴OD1∥BM.
又OD1?平面D1AC,BM?平面D1AC,
∴BM∥平面D1AC.
(2)证明 连接OB1.∵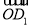 ·
·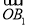 =(-1,-1,
=(-1,-1,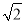 )·(1,1,
)·(1,1,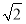 )=0,
)=0,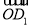 ·
·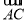 =
=
(-1,-1,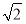 )·(-2,2,0)=0,∴
)·(-2,2,0)=0,∴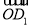 ⊥
⊥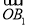 ,
,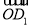 ⊥
⊥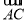 ,即OD1⊥OB1,OD1⊥AC,又OB1∩AC=O,∴D1O⊥平面AB1C.
,即OD1⊥OB1,OD1⊥AC,又OB1∩AC=O,∴D1O⊥平面AB1C.
(3)解 ∵CB⊥AB,CB⊥BB1,∴CB⊥平面ABB1,∴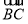 =(-2,0,0)为平面ABB1的一个法向量.由(2)知
=(-2,0,0)为平面ABB1的一个法向量.由(2)知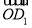 为平面AB1C的一个法向量.
为平面AB1C的一个法向量.
∴cos〈 ,
,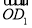 〉=
〉= ,∴
,∴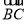 与
与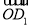 的夹角为60°,即二面角B-AB1-C的大小为60°.
的夹角为60°,即二面角B-AB1-C的大小为60°.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练4练习卷(解析版) 题型:填空题
已知函数f(x)=aln x+x在区间[2,3]上单调递增,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习7-2随机变量及其分布练习卷(解析版) 题型:解答题
以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
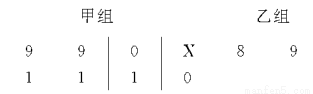
(1)如果X=8,求乙组同学植树棵数的平均数和方差;
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y的分布列和数学期望.(注:方差s2=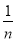 [(x1-
[(x1-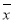 )2+(x2-
)2+(x2-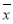 )2+…+(xn-
)2+…+(xn- )2],其中
)2],其中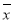 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-2椭圆、双曲线、抛物线练习卷(解析版) 题型:选择题
已知直线l过抛物线C的焦点,且与C的对称轴垂直,l与C交于A、B两点,|AB|=12,P为C的准线上一点,则△ABP的面积为( ).
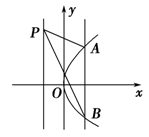
A.18 B.24 C.36 D.48
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-1直线与圆练习卷(解析版) 题型:填空题
已知直线 ax+by=1(a,b是实数)与圆O:x2+y2=1(O是坐标原点)相交于A,B两点,且△AOB是直角三角形,点P(a,b)是以点M(0,1)为圆心的圆M上的任意一点,则圆M的面积的最小值为________.
ax+by=1(a,b是实数)与圆O:x2+y2=1(O是坐标原点)相交于A,B两点,且△AOB是直角三角形,点P(a,b)是以点M(0,1)为圆心的圆M上的任意一点,则圆M的面积的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(解析版) 题型:选择题
在三棱柱ABC-A1B1C1中,各棱长相等,侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是 ( ).
A.30° B.45° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习5-1空间几何体与点等练习卷(解析版) 题型:填空题
已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习4-1等差数列与等比数列练习卷(解析版) 题型:解答题
设数列{an}的前n项和为Sn,已知ban-2n=(b-1)Sn.
(1)证明:当b=2时,{an-n·2n-1}是等比数列;
(2)求{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(解析版) 题型:填空题
已知定义在R上的函数y=f(x)满足条件f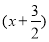 =-f(x),且函数y=f
=-f(x),且函数y=f 为奇函数,给出以下四个命题:
为奇函数,给出以下四个命题:
(1)函数f(x)是周期函数;
(2)函数f(x)的图象关于点 对称;
对称;
(3)函数f(x)为R上的偶函数;
(4)函数f(x)为R上的单调函数.
其中真命题的序号为________.(写出所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com