若平移椭圆4(x+3)2+9y2=36,使平移后的椭圆中心在第一象限,且它与x轴、y轴分别只有一个交点,则平移后的椭圆方程是 .
【答案】
分析:先把平移前椭圆的方程整理成标准方程,进而可得椭圆的长半轴的长度和短半轴的长度,进而根据平移后的椭圆中心在第一象限,且它与x轴、y轴分别只有一个交点,可得平移后椭圆的中心坐标,进而可得平移后椭圆的方程.
解答:解:先整理4(x+3)
2+9y
2=36,得
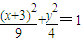
∴椭圆的长半轴为3,短半轴为2,
∵平移后的椭圆中心在第一象限,且它与x轴、y轴分别只有一个交点,
∴椭圆的中心到y轴的距离为椭圆的长半轴的长度3,到x轴的距离为短半轴的长度2
∴平移后椭圆的中心坐标(3,2),长半轴和短半轴的长度不变,
∴平移后的椭圆方程是
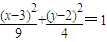 点评:
点评:本题主要考查了椭圆的标准方程和函数图象的平移.解题的关键是椭圆的长轴和短轴的长度均不变,只需求得椭圆的中心的坐标即可.

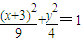
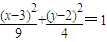


 名校课堂系列答案
名校课堂系列答案