
���� ��1����a=k=1���뺯�����������y=f��x��+g��x���ĵ������Ӷ���������ĵ������伴�ɣ�
��2���ⲻ��ʽf��m����f��1�����ɣ�
��3������ʽ�ȼ���F��x��=|f��x��|-g��x����[2��4]�ϵ�������ȻF��x��Ϊ�ֶκ�������ϵ����Զ�ÿһ�κ����������ۼ��ɣ�
��� �⣺��1��a=k=1ʱ��y=f��x��+g��x��=2x+$\frac{1}{x}$-1��x��0����
y��=2-$\frac{1}{{x}^{2}}$=$\frac{2{x}^{2}-1}{{x}^{2}}$��x��0����
��y�䣾0����ã�x��$\frac{\sqrt{2}}{2}$��x��-$\frac{\sqrt{2}}{2}$����y�䣼0����ã�-$\frac{\sqrt{2}}{2}$��x��$\frac{\sqrt{2}}{2}$��x��0��
�ʺ����ڣ�-�ޣ�-$\frac{\sqrt{2}}{2}$������$\frac{\sqrt{2}}{2}$��+�ޣ��������ڣ�-$\frac{\sqrt{2}}{2}$��0������0��$\frac{\sqrt{2}}{2}$���ݼ���
��2����a��[3��4]��
��y=f��x���ڣ�1��$\sqrt{a}$���ϵݼ����ڣ�$\sqrt{a}$��+�ޣ��ϵ�����
�֡�f��x��������[1��m]�ϵ����ֵΪf��m����
��f��m����f��1������ã�m-1����m-a����0��
��m��amax����m��4��
��3����|f��x1��|-|f��x2��|��g��x1��-g��x2����
��|f��x1��|-g��x1����|f��x2��|-g��x2���������
��F��x��=|f��x��|-g��x������F��x����[2��4]�ϵ�����
����F��x��=$\left\{\begin{array}{l}{��-1-k��x-\frac{a}{x}+1��x��[2��2+\sqrt{4-a}]}\\{��1-k��x+\frac{a}{x}-7��x�ʣ�2+\sqrt{4-a}��4]}\end{array}\right.$��
��i����x��[2��2+$\sqrt{4-a}$]ʱ��F��x��=��-1-k��x-$\frac{a}{x}$+1��
�ٵ�k=-1ʱ��F��x��=-$\frac{a}{x}$+1��[2��2+$\sqrt{4-a}$]�ϵ���������k=-1���ϣ�
�ڵ�k��-1ʱ��F��x��=��-1-k��x-$\frac{a}{x}$+1��[2��2+$\sqrt{4-a}$]�ϵ���������k��-1���ϣ�
�۵�k��-1ʱ��ֻ�� $\sqrt{\frac{a}{k+1}}$��2+$\sqrt{4-a}$���� $\sqrt{\frac{1}{k+1}}$�ݣ�$\frac{2}{\sqrt{a}}$+$\sqrt{\frac{4}{a}-1}$��max=2+$\sqrt{3}$��
����-1��k��6-4$\sqrt{3}$���Ӷ�k��6-4$\sqrt{3}$��
��ii����x�ʣ�2+$\sqrt{4-a}$��4]ʱ��F��x��=��1-k��x+$\frac{a}{x}$-7��
�ٵ�k=1ʱ��F��x��=$\frac{a}{x}$-7�ڣ�2+$\sqrt{4-a}$��4]�ϵݼ�������k=1�����ϣ�
�ڵ�k��1ʱ��F��x��=��1-k��x+$\frac{a}{x}$-7�ڣ�2+$\sqrt{4-a}$��4]�ϵݼ�������k��1�����ϣ�
�۵�k��1ʱ��ֻ�� $\sqrt{\frac{a}{1-k}}$��2+$\sqrt{4-a}$���� $\sqrt{\frac{1}{1-k}}$�ܣ�$\frac{2}{\sqrt{a}}$+$\sqrt{\frac{4}{a}-1}$��min=1+$\sqrt{2}$��
����k��2$\sqrt{2}$-2��
���Ͽ�֪��k��6-4$\sqrt{3}$��
���� �������ú����ĵ����Խ������ֵ������ʽ��������⣬������������������Լ��������۵�˼�룬�������⣮


 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��Ҷͼ��¼����ij�����������У���λ����Ϊһ��ѡ�ִ���ķ�������ȥ��һ����߷ֺ�һ����ͷֺ���ʣ���ݵ�ƽ��ֵΪ92������Ϊ2.8��
��ͼ��Ҷͼ��¼����ij�����������У���λ����Ϊһ��ѡ�ִ���ķ�������ȥ��һ����߷ֺ�һ����ͷֺ���ʣ���ݵ�ƽ��ֵΪ92������Ϊ2.8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
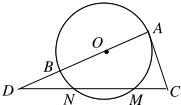 ��ͼ��ABΪ��O��ֱ����AC�С�O�ڵ�A����AC=2$\sqrt{2}$����C�ĸ���CMN��AB���ӳ����ڵ�D����CM=MN=ND����BD�ij�����$\frac{2\sqrt{7}}{7}$��
��ͼ��ABΪ��O��ֱ����AC�С�O�ڵ�A����AC=2$\sqrt{2}$����C�ĸ���CMN��AB���ӳ����ڵ�D����CM=MN=ND����BD�ij�����$\frac{2\sqrt{7}}{7}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{3}$ | B�� | $\frac{3}{5}$ | C�� | $\frac{3}{2}$ | D�� | $\frac{\sqrt{5}}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com