
分析 利用单调性的定义,进行作差,对a的值进行讨论,即可判断函数f(x)的单调性.
解答 解:f(x)=x+$\frac{a}{x}$(x>0),
设x1>x2>0,
则f(x1)-f(x2)=(x1+$\frac{a}{{x}_{1}}$)-(x2+$\frac{a}{{x}_{2}}$)
=(x1-x2)(1-$\frac{a}{{{x}_{1}x}_{2}}$),
当a>0时,若0<x2<x1≤$\sqrt{a}$,则恒有$\frac{a}{{{x}_{1}x}_{2}}$>1,
此时f(x1)-f(x2)<0,f(x)在(0,$\sqrt{a}$]上是减函数;
若x1>x2≥$\sqrt{a}$,则恒有0<$\frac{a}{{{x}_{1}x}_{2}}$<1,
此时f(x1)-f(x2)>0,f(x)在[$\sqrt{a}$,+∞)上是增函数;
当a≤0时,x1-x2>0,1-$\frac{a}{{{x}_{1}x}_{2}}$>0,
此时f(x1)-f(x2)>0,f(x)在(0,+∞)上是单调增函数;
综上,a>0时,f(x)在(0,$\sqrt{a}$]上是减函数,在[$\sqrt{a}$,+∞)上是增函数;
a≤0时,f(x)在(0,+∞)上是单调增函数.
点评 本题考查了函数的单调性的判断与证明问题,作差法是证明和判断单调性的最常用方法,是基础题目.


 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
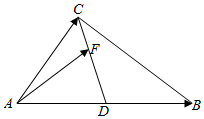 如图所示,在△ABC中,AD=DB,F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,$\overrightarrow{AF}$=$x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为$6+4\sqrt{2}$.
如图所示,在△ABC中,AD=DB,F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,$\overrightarrow{AF}$=$x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为$6+4\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
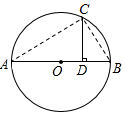 如图,已知圆的直径AB=13,C为圆上一点,过C作CD⊥AB于点D(AD>BD),若CD=6,则AD的长为( )
如图,已知圆的直径AB=13,C为圆上一点,过C作CD⊥AB于点D(AD>BD),若CD=6,则AD的长为( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
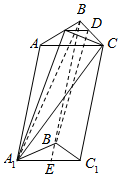 如图,三棱柱ABC-A1B1C1中,平面ABB1A1⊥平面ABC,△ABC为等边三角形,AB=$\frac{1}{2}$AA1=1,∠A1AB=120°,D,E分别是BC,A1C1的终点.
如图,三棱柱ABC-A1B1C1中,平面ABB1A1⊥平面ABC,△ABC为等边三角形,AB=$\frac{1}{2}$AA1=1,∠A1AB=120°,D,E分别是BC,A1C1的终点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com