
已知函数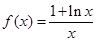 .
.
(1)若函数在区间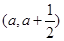 其中a >0,上存在极值,求实数a的取值范围;
其中a >0,上存在极值,求实数a的取值范围;
(2)如果当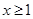 时,不等式
时,不等式 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
(1)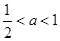 ;(2)
;(2) .
.
解析试题分析:(1)由于函数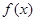 是一个确定的具体的函数,所以它的极值点也是确定的;故我们只须应用导数求出函数的极值点,注意定义域;让极值点属于区间
是一个确定的具体的函数,所以它的极值点也是确定的;故我们只须应用导数求出函数的极值点,注意定义域;让极值点属于区间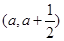 可得到关于a的不等式,从而就可求出实数a的取值范围;(2)显然不等式
可得到关于a的不等式,从而就可求出实数a的取值范围;(2)显然不等式 等价于:
等价于: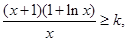 因此当
因此当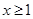 时,不等式
时,不等式 恒成立
恒成立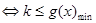 其中
其中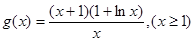 ,所以利用函数的导数求出
,所以利用函数的导数求出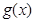 的最小值即可.
的最小值即可.
试题解析:(1)因为
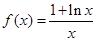 , x >0,则
, x >0,则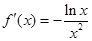 ,
,
当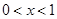 时,
时,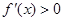 ;当
;当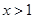 时,
时,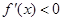 .
.
所以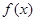 在(0,1)上单调递增;在
在(0,1)上单调递增;在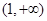 上单调递减,
上单调递减,
所以函数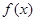 在
在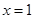 处取得极大值.
处取得极大值.
因为函数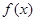 在区间
在区间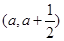 (其中
(其中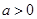 )上存在极值,
)上存在极值,
所以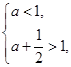 解得
解得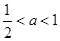 .
.
(2)不等式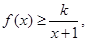 即为
即为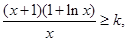 记
记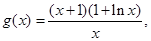
所以
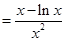
令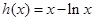 ,则
,则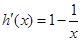 ,
, 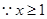 ,
, 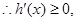
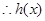 在
在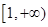 上单调递增,
上单调递增, 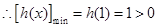 ,从而
,从而 ,
,
故 在
在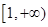 上也单调递增, 所以
上也单调递增, 所以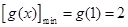 ,所以
,所以 .
.
考点:1.函数的极值与最值;2.不等式恒成立.


科目:高中数学 来源: 题型:解答题
已知函数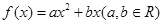 ,函数
,函数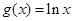 .
.
⑴当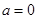 时,函数
时,函数 的图象与函数
的图象与函数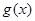 的图象有公共点,求实数
的图象有公共点,求实数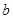 的最大值;
的最大值;
⑵当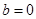 时,试判断函数
时,试判断函数 的图象与函数
的图象与函数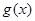 的图象的公共点的个数;
的图象的公共点的个数;
⑶函数 的图象能否恒在函数
的图象能否恒在函数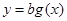 的上方?若能,求出
的上方?若能,求出 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
近年来,某企业每年消耗电费约24万元,为了节能减排,决定安装一个可使用15年的太阳能供电设备接入本企业电网,安装这种供电设备的工本费(单位:万元)与太阳能电池板的面积(单位:平方米)成正比,比例系数约为0.5.为了保证正常用电,安装后采用太阳能和电能互补供电的模式.假设在此模式下,安装后该企业每年消耗的电费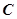 (单位:万元)与安装的这种太阳能电池板的面积
(单位:万元)与安装的这种太阳能电池板的面积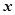 (单位:平方米)之间的函数关系是
(单位:平方米)之间的函数关系是 为常数).记
为常数).记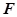 为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.
为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.
(1)试解释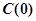 的实际意义,并建立
的实际意义,并建立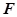 关于
关于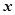 的函数关系式;
的函数关系式;
(2)当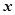 为多少平方米时,
为多少平方米时,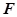 取得最小值?最小值是多少万元?
取得最小值?最小值是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com