
已知点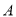 ,
,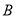 的坐标分别为
的坐标分别为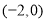 ,
,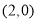 .直线
.直线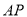 ,
,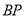 相交于点
相交于点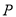 ,且它们的斜率之积是
,且它们的斜率之积是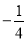 ,记动点
,记动点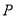 的轨迹为曲线
的轨迹为曲线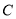 .
.
(1)求曲线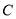 的方程;
的方程;
(2)设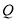 是曲线
是曲线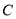 上的动点,直线
上的动点,直线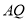 ,
,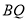 分别交直线
分别交直线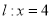 于点
于点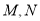 ,线段
,线段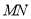 的中点为
的中点为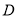 ,求直线
,求直线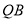 与直线
与直线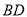 的斜率之积的取值范围;
的斜率之积的取值范围;
(3)在(2)的条件下,记直线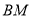 与
与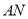 的交点为
的交点为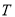 ,试探究点
,试探究点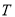 与曲线
与曲线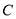 的位置关系,并说明理由.
的位置关系,并说明理由.
(1) (
( );(2)
);(2) ;(3)点
;(3)点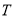 在曲线
在曲线 上.
上.
【解析】
试题分析:本题主要考查椭圆的标准方程、点斜式求直线方程、中点坐标公式等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,设出P点坐标,利用斜率公式,求出直线AP、BP的斜率,计算得到曲线C的方程;第二问,设出Q点坐标,利用点斜式写出直线AQ的方程,它与x=4交于M,则联立得到M点坐标,同理得到N点坐标,利用中点坐标公式得到 后,将Q点横坐标
后,将Q点横坐标 的范围代入直接得到所求范围;第三问,结合第二问得到直线AN和直线BM的方程,令2个方程联立,得到T点坐标,通过计算知T点坐标符合曲线C的方程,所以点T在曲线C上.
的范围代入直接得到所求范围;第三问,结合第二问得到直线AN和直线BM的方程,令2个方程联立,得到T点坐标,通过计算知T点坐标符合曲线C的方程,所以点T在曲线C上.
(1)设动点 ,则
,则 (
( 且
且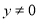 )
)
所以曲线 的方程为
的方程为 (
( ). 4分
). 4分
(2)法一:设 ,则直线
,则直线 的方程为
的方程为 ,令
,令 ,则得
,则得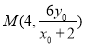 ,直线
,直线 的方程为
的方程为 ,
,
令 ,则得
,则得 , 6分
, 6分
∵ 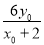
 =
=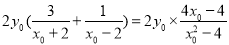
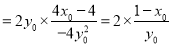
∴ ,∴
,∴  8分
8分
故


∵  ,∴
,∴ ,
,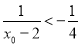
∴,
∴ ,
,
∴直线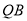 与直线
与直线 的斜率之积的取值范围为
的斜率之积的取值范围为 10分
10分
法二:设直线 的斜率为
的斜率为 ,则由题可得直线
,则由题可得直线 的斜率为
的斜率为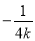 ,
,
所以直线 的方程为
的方程为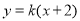 ,令
,令 ,则得
,则得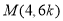 ,
,
直线 的方程为
的方程为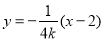 ,令
,令 ,则得
,则得 ,
,
∴ ,
,
∴  8分
8分
故


∴直线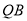 与直线
与直线 的斜率之积的取值范围为
的斜率之积的取值范围为 10分
10分
(3)法一:由(2)得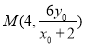 ,
, ,
,
则直线 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 , 12分
, 12分
由 ,解得
,解得 即
即  12分
12分
∴
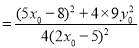



∴ 点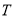 在曲线
在曲线 上. 14分
上. 14分
法二:由(2)得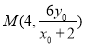 ,
,
∴  ,
, 12分
12分
∴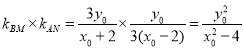

∴ 点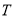 在曲线
在曲线 上. 14分
上. 14分
法三:由(2)得,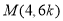 ,
, ,
,
∴ 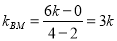 ,
, 12分
12分
∴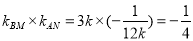 ∴ 点
∴ 点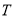 在曲线
在曲线 上. 14分
上. 14分
考点:椭圆的标准方程、点斜式求直线方程、中点坐标公式.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:填空题
已知数列{an}满足an=an-1-an-2(n≥3,n∈N*),它的前n项和为Sn.若S9=6,S10=5,则a1的值为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:填空题
某地区对两所高中学校进行学生体质状况抽测,甲校有学生800人,乙校有学生500人,现用分层抽样的方法在这1300名学生中抽取一个样本.已知在甲校抽取了48人,则在乙校应抽取学生人数为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省韶关市高三4月高考模拟(二模)理科数学试卷(解析版) 题型:填空题
若以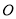 为极点,
为极点,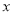 轴正半轴为极轴,曲线
轴正半轴为极轴,曲线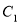 的极坐标方程为:
的极坐标方程为: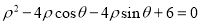 上的点到曲线
上的点到曲线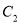 的参数方程为:
的参数方程为: (
(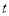 为参数)的距离的最小值为 .
为参数)的距离的最小值为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省韶关市高三4月高考模拟(二模)理科数学试卷(解析版) 题型:选择题
给出如下四个判断:
①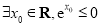 ;
;
② ;
;
③设集合 ,
, ,则“
,则“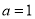 ”是“
”是“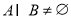 ”的必要不充分条件;
”的必要不充分条件;
④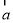 ,
,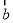 为单位向量,其夹角为
为单位向量,其夹角为 ,若
,若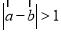 ,则
,则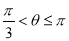 .
.
其中正确的判断个数是:( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com