
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
分析 bcosC+$\sqrt{3}$bsinC-a-c=0,利用正弦定理化简得:sinBcosC+$\sqrt{3}$sinBsinC-sinA-sinC=0,再利用和差公式、诱导公式、三角形内角和定理化简可得:$\sqrt{3}$sinB=cosB+1,进而得出.
解答 解:在△ABC中,∵bcosC+$\sqrt{3}$bsinC-a-c=0,
利用正弦定理化简得:sinBcosC+$\sqrt{3}$sinBsinC-sinA-sinC=0,
即sinBcosC+$\sqrt{3}$sinBsinC=sinA+sinC=sin(B+C)+sinC=sinBcosC+cosBsinC+sinC=sinBcosC+sinC(cosB+1),
∴$\sqrt{3}$sinB=cosB+1,即sin(B-$\frac{π}{6}$)=$\frac{1}{2}$,
∵0<B<π,∴$(B-\frac{π}{6})$∈$(-\frac{π}{6},\frac{5π}{6})$,
∴B-$\frac{π}{6}$=$\frac{π}{6}$,即B=$\frac{π}{3}$.
故选:B.
点评 本题考查了正弦定理、和差公式、和差公式、诱导公式、三角形内角和定理,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 4$\sqrt{10}$ | C. | 14 | D. | 8+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
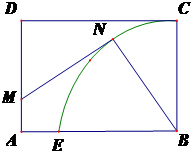 如图,某城市小区有一个矩形休闲广场,AB=20米,广场的一角是半径为16米的扇形BCE绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅MN(宽度不计),点M在线段AD上,并且与曲线CE相切;另一排为单人弧形椅沿曲线CN(宽度不计)摆放.已知双人靠背直排椅的造价每米为2a元,单人弧形椅的造价每米为a元,记锐角∠NBE=θ,总造价为W元.
如图,某城市小区有一个矩形休闲广场,AB=20米,广场的一角是半径为16米的扇形BCE绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅MN(宽度不计),点M在线段AD上,并且与曲线CE相切;另一排为单人弧形椅沿曲线CN(宽度不计)摆放.已知双人靠背直排椅的造价每米为2a元,单人弧形椅的造价每米为a元,记锐角∠NBE=θ,总造价为W元.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\sqrt{2},2)$ | B. | $(2,\sqrt{6})$ | C. | $(\sqrt{2},\sqrt{3})$ | D. | $(\sqrt{6},4)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
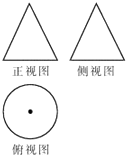 已知一个几何体的三视图如图所示,其中正视图和侧视图都是底边长为6,腰长为10的等腰三角形,俯视图是半径为3的圆,则这个几何体的表面积是( )
已知一个几何体的三视图如图所示,其中正视图和侧视图都是底边长为6,腰长为10的等腰三角形,俯视图是半径为3的圆,则这个几何体的表面积是( )| A. | 69π | B. | 24π | C. | 30π | D. | 39π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 使用年限 | 2 | 3 | 4 | 5 | 6 |
| 维修费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
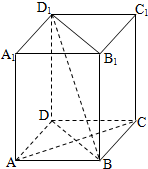 如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,
如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com