
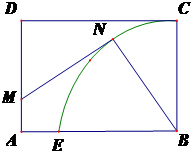
 如图,某城市小区有一个矩形休闲广场,AB=20米,广场的一角是半径为16米的扇形BCE绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅MN(宽度不计),点M在线段AD上,并且与曲线CE相切;另一排为单人弧形椅沿曲线CN(宽度不计)摆放.已知双人靠背直排椅的造价每米为2a元,单人弧形椅的造价每米为a元,记锐角∠NBE=θ,总造价为W元.
如图,某城市小区有一个矩形休闲广场,AB=20米,广场的一角是半径为16米的扇形BCE绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅MN(宽度不计),点M在线段AD上,并且与曲线CE相切;另一排为单人弧形椅沿曲线CN(宽度不计)摆放.已知双人靠背直排椅的造价每米为2a元,单人弧形椅的造价每米为a元,记锐角∠NBE=θ,总造价为W元.分析 (1)过N作AB的垂线,垂足为F;过M作NF的垂线,垂足为G.构建直角三角形,通过解直角三角形、勾股定理和弧长公式进行解答;
(2)将(1)中的函数关系进行变形得到${W^,}(θ)=8a\frac{(2cosθ-1)(cosθ-2)}{{{{sin}^2}θ}}$.W′(θ)=0,$cosθ=\frac{1}{2}$,因为$({θ_1},\frac{π}{2})$,所以$θ=\frac{π}{3}$.然后结合θ的取值范围进行分类讨论,利用三角函数的单调性进行解答.
解答  解:(1)过N作AB的垂线,垂足为F;过M作NF的垂线,垂足为G.
解:(1)过N作AB的垂线,垂足为F;过M作NF的垂线,垂足为G.
在Rt△BNF中,BF=16cosθ,则MG=20-16cosθ
在Rt△MNG中,$MN=\frac{20-16cosθ}{sinθ}$,
由题意易得$CN=16(\frac{π}{2}-θ)$,
因此,$W(θ)=2a•\frac{20-16cosθ}{sinθ}+16a(\frac{π}{2}-θ)$,$cosθ∈(0,\frac{4}{5}]$;
(2)${W^,}(θ)=-16a+8a\frac{4-5cosθ}{{{{sin}^2}θ}}\;=8a\frac{(2cosθ-1)(cosθ-2)}{{{{sin}^2}θ}}$
令W′(θ)=0,$cosθ=\frac{1}{2}$,因为$({θ_1},\frac{π}{2})$,所以$θ=\frac{π}{3}$.
设锐角θ1满足$cos{θ_1}=\frac{4}{5}$,${θ_1}∈(0,\frac{π}{3})$
当$θ∈({θ_1},\frac{π}{3})$时,W,(θ)<0,W(θ)单调递减;
当$θ∈(\frac{π}{3},\frac{π}{2})$时,W,(θ)>0,W(θ)单调递增.
所以当$θ=\frac{π}{3}$,总造价W最小,最小值为$(16\sqrt{3}+\frac{8π}{3})a$,
此时$MN=8\sqrt{3}$,$NG=4\sqrt{3}$,$NF=8\sqrt{3}$,
因此当$AM=4\sqrt{3}$米时,能使总造价最小.
点评 本题考查的知识点是在实际问题中建立三角函数模型及解三角形,根据已知条件构造出W关于θ的函数,是解答本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 初一年级 | 平均值为2,方差为2 |
| 初二年级 | 平均值为1,方差大于0 |
| 高一年级 | 中位数为3,众数为4 |
| 高二年级 | 平均值为3,中位数为4 |
| A. | 初一年级 | B. | 初二年级 | C. | 高一年级 | D. | 高二年级 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,3) | B. | [-3,+∞) | C. | (-3,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com