
分析 (1)∈N是x∈M的必要条件,所以M⊆N,当a=1时,解集N为空集,不满足,当a>1时,求得解集,列不等式组即可求得a的取值范围;
(2)方程x2-x-m=0在(-1,1)上有解,m的取值集合就是函数y=x2-x=(x-$\frac{1}{2}$)2-$\frac{1}{4}$在(-1,1)上的值域,根据二次函数性质,即可求得实数m的取值范围.
解答 解:(1)因为x∈N是x∈M的必要条件,所以M⊆N,
当a=1时,解集N为空集、不满足题意;
当a>1时,a>2-a,此时集合N={x|2-a<x<a},
则$\left\{{\begin{array}{l}{2-a<-\frac{1}{4}}\\{a≥2}\end{array}}\right.$,
所以$a>\frac{9}{4}$;
(2)由题意得,方程x2-x-m=0在(-1,1)上有解,
∴m的取值集合就是函数y=x2-x=(x-$\frac{1}{2}$)2-$\frac{1}{4}$在(-1,1)上的值域,值域为[-$\frac{1}{4}$,2),
∴实数m的取值范围[-$\frac{1}{4}$,2).
点评 本题考查充分条件和必要条件的判断,考查集合的运算,一元二次函数的性质,考查分析问题及解决问题的能力,属于中档题.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
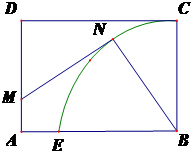 如图,某城市小区有一个矩形休闲广场,AB=20米,广场的一角是半径为16米的扇形BCE绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅MN(宽度不计),点M在线段AD上,并且与曲线CE相切;另一排为单人弧形椅沿曲线CN(宽度不计)摆放.已知双人靠背直排椅的造价每米为2a元,单人弧形椅的造价每米为a元,记锐角∠NBE=θ,总造价为W元.
如图,某城市小区有一个矩形休闲广场,AB=20米,广场的一角是半径为16米的扇形BCE绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅MN(宽度不计),点M在线段AD上,并且与曲线CE相切;另一排为单人弧形椅沿曲线CN(宽度不计)摆放.已知双人靠背直排椅的造价每米为2a元,单人弧形椅的造价每米为a元,记锐角∠NBE=θ,总造价为W元.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
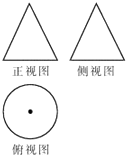 已知一个几何体的三视图如图所示,其中正视图和侧视图都是底边长为6,腰长为10的等腰三角形,俯视图是半径为3的圆,则这个几何体的表面积是( )
已知一个几何体的三视图如图所示,其中正视图和侧视图都是底边长为6,腰长为10的等腰三角形,俯视图是半径为3的圆,则这个几何体的表面积是( )| A. | 69π | B. | 24π | C. | 30π | D. | 39π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 使用年限 | 2 | 3 | 4 | 5 | 6 |
| 维修费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
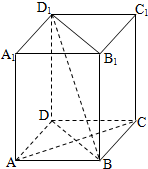 如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,
如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com