
| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
分析 求出S的三种结果,得出Smin,对②③④⑤进行分析得出答案.
解答 解:①∵xi,yi(i=1,2,3,4,5)均由2个$\overrightarrow{a}$和3个$\overrightarrow{b}$排列而成,
∴S=xiyi可能情况有三种:①S=2$\overrightarrow{a}$2+3$\overrightarrow{b}$2;②S=${\overrightarrow{a}}^{2}$+2$\overrightarrow{a}•\overrightarrow{b}$+2${\overrightarrow{b}}^{2}$;③S=4$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$.故①错误;
②∵S1-S2=S2-S3=${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$-2$\overrightarrow{a}•\overrightarrow{b}$≥${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$-2|$\overrightarrow{a}$||$\overrightarrow{b}$|=(|$\overrightarrow{a}$|-|$\overrightarrow{b}$|)2≥0,
∴S中最小为S3;
若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则Smin=S3=${\overrightarrow{b}}^{2}$,与|$\overrightarrow{a}$|无关,故②正确;
③若$\overrightarrow{a}$∥$\overrightarrow{b}$,则Smin=S3=4$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2,与|$\overrightarrow{b}$|有关,故③错误;
④若|$\overrightarrow{b}$|>4|$\overrightarrow{a}$|,则Smin=S3=4|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ+$\overrightarrow{b}$2>-4|$\overrightarrow{a}$|•|$\overrightarrow{b}$|+$\overrightarrow{b}$2>-|$\overrightarrow{b}$|2+$\overrightarrow{b}$2=0,故④正确;
⑤若|$\overrightarrow{b}$|=2|$\overrightarrow{a}$|,Smin=S3=8|$\overrightarrow{a}$|2cosθ+4|$\overrightarrow{a}$|2=8|$\overrightarrow{a}$|2,
∴2cosθ=1,∴θ=$\frac{π}{3}$,
即$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$.
综上所述,命题正确的是②④,
故选:D.
点评 本题考查命题的真假判断与应用,着重考查平面向量的数量积的综合应用,考查推理、分析与运算的综合应用,属于难题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 7 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
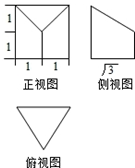
| A. | 10 | B. | $4+3\sqrt{3}$ | C. | $\frac{{5\sqrt{3}}}{3}$ | D. | $12+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 4$\sqrt{10}$ | C. | 14 | D. | 8+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
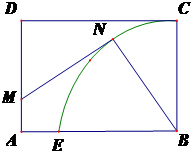 如图,某城市小区有一个矩形休闲广场,AB=20米,广场的一角是半径为16米的扇形BCE绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅MN(宽度不计),点M在线段AD上,并且与曲线CE相切;另一排为单人弧形椅沿曲线CN(宽度不计)摆放.已知双人靠背直排椅的造价每米为2a元,单人弧形椅的造价每米为a元,记锐角∠NBE=θ,总造价为W元.
如图,某城市小区有一个矩形休闲广场,AB=20米,广场的一角是半径为16米的扇形BCE绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅MN(宽度不计),点M在线段AD上,并且与曲线CE相切;另一排为单人弧形椅沿曲线CN(宽度不计)摆放.已知双人靠背直排椅的造价每米为2a元,单人弧形椅的造价每米为a元,记锐角∠NBE=θ,总造价为W元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com