
分析 (1)讨论2x-3和2x+1的正负化简绝对值代入到f(x)≤6中,求出并集即可;
(2)|2x+1︳+|2x-3︳≥|2x+1-2x+3︳=4,关于x的不等式|a-1︳<f(x)的解集为R,所以|a-1︳<4,即可求出a的取值范围.
解答 解:(1)①当x≥$\frac{3}{2}$时,解得x≤2,所以$\frac{3}{2}$≤x≤2;
②x≤-$\frac{1}{2}$时,解得x≥-1,所以-1$≤x≤-\frac{1}{2}$;
③当-$\frac{1}{2}$$<x<\frac{3}{2}$时,解得x∈R,所以-$\frac{1}{2}$$<x<\frac{3}{2}$;
综上:不等式的解集为x|-1≤x≤2};
(2)因为|2x+1︳+|2x-3︳≥|2x+1-2x+3︳=4,关于x的不等式|a-1︳<f(x)的解集为R,
所以,|a-1︳<4,解得-3<a<5 …(10分)
点评 考查学生理解函数恒成立时所取的条件,以及会分情况讨论求出绝对值不等式的解集.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
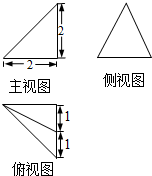
| A. | $\frac{{41\sqrt{41}π}}{48}$ | B. | 12π | C. | $\frac{25π}{4}$ | D. | $\frac{41π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com