
分析 由已知列式求得t,得到$\overrightarrow{a}+\overrightarrow{b}$的坐标,由模的公式得答案.
解答 解:由$\overrightarrow a=(-1,3)$,$\overrightarrow b=(1,t)$,得$\overrightarrow{a}-2\overrightarrow{b}$=(-3,3-2t),
若$(\overrightarrow a-2\overrightarrow b)⊥\overrightarrow a$,则-1×(-3)+3(3-2t)=0,解得t=2,
∴$\overrightarrow{b}=(1,2)$,则$\overrightarrow{a}+\overrightarrow{b}=(0,5)$,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=5.
故答案为:5.
点评 本题考查平面向量的数量积运算,考查了向量模的求法,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
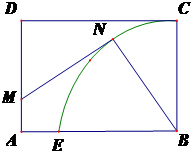 如图,某城市小区有一个矩形休闲广场,AB=20米,广场的一角是半径为16米的扇形BCE绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅MN(宽度不计),点M在线段AD上,并且与曲线CE相切;另一排为单人弧形椅沿曲线CN(宽度不计)摆放.已知双人靠背直排椅的造价每米为2a元,单人弧形椅的造价每米为a元,记锐角∠NBE=θ,总造价为W元.
如图,某城市小区有一个矩形休闲广场,AB=20米,广场的一角是半径为16米的扇形BCE绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅MN(宽度不计),点M在线段AD上,并且与曲线CE相切;另一排为单人弧形椅沿曲线CN(宽度不计)摆放.已知双人靠背直排椅的造价每米为2a元,单人弧形椅的造价每米为a元,记锐角∠NBE=θ,总造价为W元.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
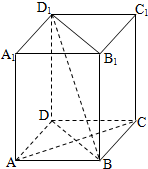 如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,
如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com