
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
分析 由三角形垂心的性质,得BF⊥OA,即kBF•kOA=-1,由此可得C1的离心率.
解答 解:联立渐近线与抛物线方程得A($\frac{2pb}{a}$,$\frac{2p{b}^{2}}{{a}^{2}}$),B(-$\frac{2pb}{a}$,$\frac{2p{b}^{2}}{{a}^{2}}$),抛物线焦点为F(0,$\frac{p}{2}$),
由三角形垂心的性质,得BF⊥OA,即kBF•kOA=-1,
所以$(\frac{a}{4b}-\frac{b}{a})\frac{b}{a}$-1,所以b=$\frac{\sqrt{5}}{2}$a,
所以c=$\frac{3}{2}$a,所以C1的离心率为$\frac{3}{2}$.
故选:B.
点评 本题考查双曲线的性质,联立方程组,根据三角形垂心的性质,得BF⊥OA是解决本题的关键,考查学生的计算能力.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:选择题
| 初一年级 | 平均值为2,方差为2 |
| 初二年级 | 平均值为1,方差大于0 |
| 高一年级 | 中位数为3,众数为4 |
| 高二年级 | 平均值为3,中位数为4 |
| A. | 初一年级 | B. | 初二年级 | C. | 高一年级 | D. | 高二年级 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
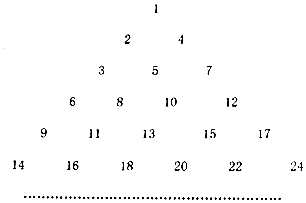 把正整数按一定的规则排成了如图所示的三角形数表,设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,如a42=8,若aij=2015,则i+j=110?.
把正整数按一定的规则排成了如图所示的三角形数表,设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,如a42=8,若aij=2015,则i+j=110?.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com