
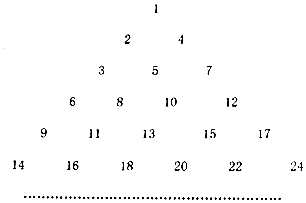
 把正整数按一定的规则排成了如图所示的三角形数表,设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,如a42=8,若aij=2015,则i+j=110?.
把正整数按一定的规则排成了如图所示的三角形数表,设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,如a42=8,若aij=2015,则i+j=110?. 分析 通过观察给出的三角形数表,找到如下规律,奇数行都是奇数,偶数行都是偶数,且每一行的数的个数就是行数,然后根据2015是第1008个奇数,利用等差数列的前n项和公式分析出它所在的行数,再利用等差数列的通项公式求其所在的列数,则i与j的和可求.
解答 解:由三角形数表可以看出其奇数行中的数都是奇数,偶数行中的数都是偶数,
2015=2×1008-1,所以2015为第1008个奇数,
又每一行中奇数的个数就是行数,又前31个奇数行内奇数的个数的和为31×$1+\frac{31×(31-1)×2}{2}$=961,
即第31个奇数行的最后一个奇数是961×2-1=1921,前32个奇数行内奇数的个数的和为32×1+$\frac{32×(32-1)×2}{2}$=1024,
故2015在第32个奇数行内,
所以i=63,因为第63行的第一个数为1923,则2015=1923+2(m-1),所以m=47,
即j=47,所以i+j=63+47=110.
故答案为:110.
点评 本题考查了等差数列的通项公式和前n项和公式,考查了观察和分析图表的能力,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | $(\sqrt{2},2)$ | B. | $(2,\sqrt{6})$ | C. | $(\sqrt{2},\sqrt{3})$ | D. | $(\sqrt{6},4)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 使用年限 | 2 | 3 | 4 | 5 | 6 |
| 维修费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | 5 | C. | $\frac{11}{2}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
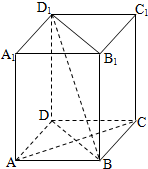 如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,
如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com