
分析 (1)利用已知条件,结合数列的定义证明求解即可.
(2)直接利用拆项法,分别通过等差数列以及等比数列求和求解即可.
解答 解:(1)∵a1=1,an+1=3an+4n-2,(n∈N+),
∴$\frac{{{a_{n+1}}+2(n+1)}}{{{a_n}+2n}}=\frac{{3{a_n}+4n-2+2(n+1)}}{{{a_n}+2n}}=\frac{{3({a_n}+2n)}}{{{a_n}+2n}}=3$,
∴{an+2n}是以a1+2=3为首项,以q=3公比的等比数列.
∴${a_n}+2n={3^n}⇒{a_n}={3^n}-2n$,
(2)${S_n}={a_1}+{a_2}+{a_3}+…+{a_n}=({3^1}-2)+({3^2}-4)+({3^3}-6)+…+({3^n}-2n)$=$({3^1}+{3^2}+{3^3}+…+{3^n})-(2+4+6+8+…+2n)=\frac{{{3^{n+1}}-3}}{2}-({n^2}+n)$.
点评 本题考查数列的递推关系式的应用,数列求和,考查计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
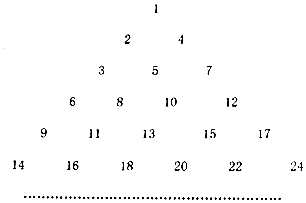 把正整数按一定的规则排成了如图所示的三角形数表,设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,如a42=8,若aij=2015,则i+j=110?.
把正整数按一定的规则排成了如图所示的三角形数表,设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,如a42=8,若aij=2015,则i+j=110?.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com