
分析 (1)由题意画出图形,列出关于a,b,c的方程组,求解方程组得到a,b的值,则椭圆方程可求;
(2)设出过点P的直线的参数方程,与椭圆方程联立,化为关于t的一元二次方程,利用根与系数的关系即可求得|PA|•|PB|的取值范围.
解答 解:(1)如图,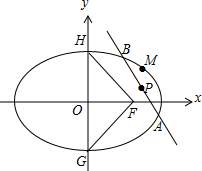 由题意设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,
由题意设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,
则$\left\{\begin{array}{l}{b=c}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{4}{{a}^{2}}+\frac{2}{{b}^{2}}=1}\end{array}\right.$,解得a2=8,b2=4.
∴椭圆方程为:$\frac{x^2}{8}+\frac{y^2}{4}=1$;
(2)设过点P的直线的参数方程为$\left\{{\begin{array}{l}{x=2+tcosα}\\{y=1+tsinα}\end{array}}\right.(t为参数)$,
代入椭圆方程并整理得t2(cos2α+2sin2α)+4t(cocα+sinα)-2=0.
则${t_1}{t_2}=\frac{-2}{{{{cos}^2}α+2{{sin}^2}α}}$,
∴|PA||PB|=$\frac{2}{co{s}^{2}α+2si{n}^{2}α}=\frac{2}{1+si{n}^{2}α}$∈[1,2].
点评 本题考查椭圆方程的求法,考查了椭圆的简单性质,训练了利用参数方程求解直线与椭圆的相交关系问题,是中档题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:解答题
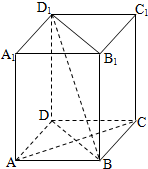 如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,
如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com