
分析 分别用三角函数的范围和奇偶性,三角函数的图象和诱导公式以及向量共线知识进行逐项判断.
解答 解:对于①、sinαcosα=1;可得sin2α=2,由sin2α∈[-1,1],故①不对;
对于②、因$y=sin(\frac{3π}{2}+x)$=-cosx,所以此函数是偶函数,故②对;
对于③、把$x=\frac{π}{8}$代入$y=sin(\frac{5π}{4}+2x)$=sin$\frac{3π}{2}$=-1,解得y=-1,故③对;
对于④、如α=2π+$\frac{π}{6}$,β=$\frac{π}{3}$时,有sinα<sinβ,故④不对;
对于⑤、如果$\overrightarrow{b}=\overrightarrow{0}$,$\overrightarrow{a}$、$\overrightarrow{c}$是非零向量,$\overrightarrow{a}$∥$\overrightarrow{b}$,$\overrightarrow{b}$∥$\overrightarrow{c}$,则$\overrightarrow{a}$∥$\overrightarrow{c}$不一定成立;故⑤不对;
故答案为:②③.
点评 本题考查了三角函数的定义、图象和性质以及诱导公式,向量共线等等有关知识,考查的知识多、范围广,但是难度不大是对基础概念的理解和应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | [-3,3) | B. | [-3,+∞) | C. | (-3,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网格纸上小正方形的边长为1,粗实线画出的是某空间几何体的三视图,则下列说法错误的是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某空间几何体的三视图,则下列说法错误的是( )| A. | 该几何体的体积为16 | B. | 该几何体的表面积为36 | ||
| C. | 该几何体的最长棱为$\sqrt{41}$ | D. | 该几何体外接球的表面积为41π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,梯形ABCD中,AB∥CD,BE⊥CD,DE=BE=CE=2AB,将ABED沿BE边翻折,使平面ABED⊥平面BCE,M是BC的中点,点N在线段DE上且满足DN=$\frac{1}{4}$DE.
如图,梯形ABCD中,AB∥CD,BE⊥CD,DE=BE=CE=2AB,将ABED沿BE边翻折,使平面ABED⊥平面BCE,M是BC的中点,点N在线段DE上且满足DN=$\frac{1}{4}$DE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 空气质量指数 | (0,35] | (35,75] | (75,115] | (115,150] | (150,250] | >250 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 甲区天数 | 13 | 20 | 42 | 20 | 3 | 2 |
| 乙区天数 | 8 | 32 | 40 | 16 | 2 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
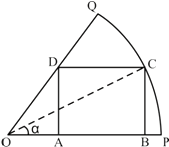 某一扇型的铁皮,半径长为1,圆心角为$\frac{π}{3}$,今想从中剪下一个矩形ABCD,如图所示,设∠COP=α,试问当α取何值时,矩形ABCD的面积最大,并求出这个最大值.
某一扇型的铁皮,半径长为1,圆心角为$\frac{π}{3}$,今想从中剪下一个矩形ABCD,如图所示,设∠COP=α,试问当α取何值时,矩形ABCD的面积最大,并求出这个最大值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(0,2] | B. | [-2,0)∪(0,2] | C. | [-2,2] | D. | (-1,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com