
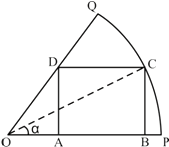
 某一扇型的铁皮,半径长为1,圆心角为$\frac{π}{3}$,今想从中剪下一个矩形ABCD,如图所示,设∠COP=α,试问当α取何值时,矩形ABCD的面积最大,并求出这个最大值.
某一扇型的铁皮,半径长为1,圆心角为$\frac{π}{3}$,今想从中剪下一个矩形ABCD,如图所示,设∠COP=α,试问当α取何值时,矩形ABCD的面积最大,并求出这个最大值. 分析 先用α把矩形的各边长表示出来,进而表示矩形的面积,化简,利用α的范围,集合三角函数的性质求解.
解答 解:∵△OBC是直角三角形,
∴在Rt△OBC中,由OB=OC•cosα=cosα;BC=OC•sinα=sinα;
又∵△OAD是直角三角形,
在Rt△OAD中,
∵$\frac{AD}{OA}=tan60°=\sqrt{3}$,
∴OA=$\frac{\sqrt{3}}{3}BC$=$\frac{\sqrt{3}}{3}$sinα;
又∵AB=OB-OA=cosα-$\frac{\sqrt{3}}{3}$sinα.
所以:矩形ABCD的面积等于AB•BC:
令f(α)=AB•BC=(cosα-$\frac{\sqrt{3}}{3}$sinα)•sinα
化简得:f(α)=$\frac{\sqrt{3}}{3}sin(2α+\frac{π}{6})-\frac{\sqrt{3}}{6}$
∵$0<α<\frac{π}{3}$
∴$\frac{π}{6}<2α+\frac{π}{6}<\frac{5π}{6}$,
当$2α+\frac{π}{6}=\frac{π}{2}$,即$α=\frac{π}{6}$时,函数f(α)取得最大值,即矩形ABCD的面积最大,最大值为$\frac{\sqrt{3}}{6}$.
点评 本题考查了三角函数在实际生活中的运用,解题的关键就是关键图形建立三角模型,利用三角函数的性质解题.属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [60°,120°] | B. | [30°,150°] | ||
| C. | (0°,60°]∪[120°,180°) | D. | [60°,90°)∪(90°,120°] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com