
| A. | [60°,120°] | B. | [30°,150°] | ||
| C. | (0°,60°]∪[120°,180°) | D. | [60°,90°)∪(90°,120°] |
分析 根据直线和圆的位置关系即可得到结论.
解答 解:若直线斜率不存在,此时x=0与圆有交点,
直线斜率存在,设为k,则过P的直线方程为y=kx-2,
即kx-y-2=0,
若过点(0,-2)的直线l与圆x2+y2=1有公共点,
则圆心到直线的距离d≤1,
即$\frac{2}{\sqrt{{k}^{2}+1}}$≤1,即k2-3≥0,
解得k≤-$\sqrt{3}$或k≥$\sqrt{3}$,
即60°≤α≤120°且α≠90°,
综上所述,60°≤α≤120°,
故选:A.
点评 本题主要考查直线和圆的位置关系的应用以及直线倾斜角的求解,根据条件转化为圆心到直线的距离和半径之间的关系是解决本题的关键.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
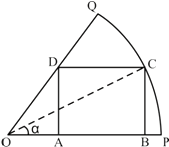 某一扇型的铁皮,半径长为1,圆心角为$\frac{π}{3}$,今想从中剪下一个矩形ABCD,如图所示,设∠COP=α,试问当α取何值时,矩形ABCD的面积最大,并求出这个最大值.
某一扇型的铁皮,半径长为1,圆心角为$\frac{π}{3}$,今想从中剪下一个矩形ABCD,如图所示,设∠COP=α,试问当α取何值时,矩形ABCD的面积最大,并求出这个最大值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(0,2] | B. | [-2,0)∪(0,2] | C. | [-2,2] | D. | (-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (5x)′=5x | B. | (logax)'=$\frac{lna}{x}$ | C. | (5x)′=5xln5 | D. | (logax)'=$\frac{a}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>b2 | B. | ${a^{\frac{1}{2}}}$>${b^{\frac{1}{2}}}$ | C. | a-3<b-3 | D. | ${a^{\frac{1}{3}}}$>${b^{\frac{1}{3}}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com