
分析 由已知求出数列的通项公式,然后利用数学归纳法证明$\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}+…+\frac{1}{{{a_{2^n}}}}$≥$\frac{n+2}{2}$.
解答 解:$\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}+…+\frac{1}{{{a_{2^n}}}}$≥$\frac{n+2}{2}$.
证明如下:由an+1-an=1,a1=1,知数列{an}为首项是1,公差为1的等差数列,
∴通项公式为an=n.
要证$\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}+…+\frac{1}{{{a_{2^n}}}}$≥$\frac{n+2}{2}$,
只要证:1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{n}}$≥$\frac{n+2}{2}$,下面用数学归纳证明:
n=1时,1+$\frac{1}{2}$=$\frac{1+2}{2}$,结论成立,
当n=2时,左边=1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$=$\frac{25}{12}$$>\frac{24}{12}=2$,结论成立;
假设n=k时结论成立,即1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{k}}$≥$\frac{k+2}{2}$,
那么:n=k+1时,1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{k}}+\frac{1}{{2}^{k}+1}$+…+$\frac{1}{{2}^{k+1}}$>$\frac{k+2}{2}$+$\frac{1}{{2}^{k}}$+…+$\frac{1}{{2}^{k+1}}$
>$\frac{k+2}{2}$+$\frac{1}{{2}^{k+1}}+\frac{1}{{2}^{k+1}}$+…+$\frac{1}{{2}^{k+1}}$>$\frac{k+2}{2}$+$\frac{{2}^{k}}{{2}^{k+1}}$=$\frac{k+3}{2}$,即n=k+1时,结论也成立.
综上所述,n∈N,结论成立.
点评 本题是数列与不等式的综合题,考查了数学归纳法与放缩法证明数列不等式,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 非充分非必要条件 | D. | 充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,梯形ABCD中,AB∥CD,BE⊥CD,DE=BE=CE=2AB,将ABED沿BE边翻折,使平面ABED⊥平面BCE,M是BC的中点,点N在线段DE上且满足DN=$\frac{1}{4}$DE.
如图,梯形ABCD中,AB∥CD,BE⊥CD,DE=BE=CE=2AB,将ABED沿BE边翻折,使平面ABED⊥平面BCE,M是BC的中点,点N在线段DE上且满足DN=$\frac{1}{4}$DE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 空气质量指数 | (0,35] | (35,75] | (75,115] | (115,150] | (150,250] | >250 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 甲区天数 | 13 | 20 | 42 | 20 | 3 | 2 |
| 乙区天数 | 8 | 32 | 40 | 16 | 2 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
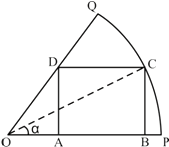 某一扇型的铁皮,半径长为1,圆心角为$\frac{π}{3}$,今想从中剪下一个矩形ABCD,如图所示,设∠COP=α,试问当α取何值时,矩形ABCD的面积最大,并求出这个最大值.
某一扇型的铁皮,半径长为1,圆心角为$\frac{π}{3}$,今想从中剪下一个矩形ABCD,如图所示,设∠COP=α,试问当α取何值时,矩形ABCD的面积最大,并求出这个最大值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 第x年 | 1 | 2 | 3 | 4 | 5 |
| 需求量(万吨) | 3 | 6 | 5 | 7 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com