
【题目】定义在R上的偶函数f(x)满足f(x)+f(x+1)=0,且在[﹣3,﹣2]上f(x)=2x+5,A、B是三边不等的锐角三角形的两内角,则下列不等式正确的是( )
A.f(sinA)>f(sinB)
B.f(cosA)>f(cosB)
C.f(sinA)>f(cosB)
D.f(sinA)<f(cosB)
【答案】D
【解析】解:由f(x)+f(x+1)=0,
∴f(x+2)=f(x),
∴函数的周期为2,
∵f(x)在[﹣3,﹣2]上为增函数,
∴f(x)在[﹣1,0]上为增函数,
∵f(x)为偶函数,
∴f(x)在[0,1]上为单调减函数.
∵在锐角三角形中,π﹣A﹣B< ![]() ,
,
∴A+B> ![]() ,
,
∴ ![]() ﹣B<A,
﹣B<A,
∵A,B是锐角,
∴0< ![]() ﹣B<A<
﹣B<A< ![]() ,
,
∴sinA>sin( ![]() ﹣B)=cosB,
﹣B)=cosB,
∴f(x)在[0,1]上为单调减函数.
∴f(sinA)<f(cosB),
故选D.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知a>0且a≠1,设
命题p:函数y=logax在区间(0,+∞)内单调递减;
q:曲线y=x2+(2a﹣3)x+1与x轴有两个不同的交点,
如果p∧q为真命题,试求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线y2=2px(p>0)的焦点,斜率为2 ![]() 的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若 ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(﹣3,1),
=(﹣3,1), ![]() =(1,﹣2),
=(1,﹣2), ![]() =
= ![]() +k
+k ![]() (k∈R).
(k∈R).
(1)若 ![]() 与向量2
与向量2 ![]() ﹣
﹣ ![]() 垂直,求实数k的值;
垂直,求实数k的值;
(2)若向量 ![]() =(1,﹣1),且
=(1,﹣1),且 ![]() 与向量k
与向量k ![]() +
+ ![]() 平行,求实数k的值.
平行,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cos
=(cos ![]() ,sin
,sin ![]() ),
), ![]() =(cos
=(cos ![]() ,﹣sin
,﹣sin ![]() ),函数f(x)=
),函数f(x)= ![]()
![]() ﹣m|
﹣m| ![]() +
+ ![]() |+1,x∈[﹣
|+1,x∈[﹣ ![]() ,
, ![]() ],m∈R.
],m∈R.
(1)当m=0时,求f( ![]() )的值;
)的值;
(2)若f(x)的最小值为﹣1,求实数m的值;
(3)是否存在实数m,使函数g(x)=f(x)+ ![]() m2 , x∈[﹣
m2 , x∈[﹣ ![]() ,
, ![]() ]有四个不同的零点?若存在,求出m的取值范围;若不存在,说明理由.
]有四个不同的零点?若存在,求出m的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某工厂对一批新产品长度(单位:mm)检测结果的频率分布直方图.估计这批产品的中位数为( ) 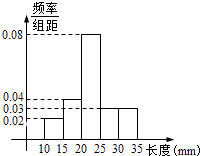
A.20
B.25
C.22.5
D.22.75
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)对于定义域内的任意x都满足 ![]() ,则称f(x)具有性质M.
,则称f(x)具有性质M.
(1)很明显,函数 ![]() (x∈(0,+∞)具有性质M;请证明
(x∈(0,+∞)具有性质M;请证明 ![]() (x∈(0,+∞)在(0,1)上是减函数,在(1,+∞)上是增函数.
(x∈(0,+∞)在(0,1)上是减函数,在(1,+∞)上是增函数.
(2)已知函数g(x)=|lnx|,点A(1,0),直线y=t(t>0)与g(x)的图象相交于B、C两点(B在左边),验证函数g(x)具有性质M并证明|AB|<|AC|.
(3)已知函数 ![]() ,是否存在正数m,n,k,当h(x)的定义域为[m,n]时,其值域为[km,kn],若存在,求k的范围,若不存在,请说明理由.
,是否存在正数m,n,k,当h(x)的定义域为[m,n]时,其值域为[km,kn],若存在,求k的范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,C上一点(3,m)到焦点的距离为5.
(1)求C的方程;
(2)过F作直线l,交C于A、B两点,若线段AB中点的纵坐标为﹣1,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com