

 ,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用
,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用 分别表示在第
分别表示在第 次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数. ,分别求出第二次,第三次选“音乐欣赏”课的人数
,分别求出第二次,第三次选“音乐欣赏”课的人数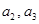 ;
; 是等比数列,并用
是等比数列,并用 表示
表示 ;
; 的取值范围.
的取值范围. ,
, (2)①
(2)①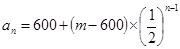 ②
② ,且
,且
 ,分别取
,分别取 ,即可求出
,即可求出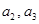 ,(2)①由题意得
,(2)①由题意得 ,由
,由 ,代入
,代入 即可得证;②前十次听“音乐欣赏”课的学生总人次即为数列
即可得证;②前十次听“音乐欣赏”课的学生总人次即为数列 的前10项和
的前10项和 ,根据题意,
,根据题意, ,由已知,
,由已知, ,得
,得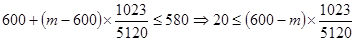 ,解之即可.
,解之即可. ,又
,又 ,
, ,
,  ,
,  ,
,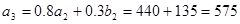 .
. ,
, ,
, 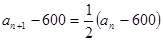 ,
, 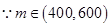 ,∴
,∴ ,
, 是等比数列,公比为
是等比数列,公比为 首项为
首项为
 ,
,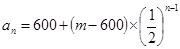
 的前10项和
的前10项和 ,
, ,
,  ,得
,得 ,
, ,∴
,∴ ,
, ,∴
,∴ 的取值范围是
的取值范围是 ,且
,且 .
.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com