已知正项数列{a
n}的前n项和为S
n,若2S
n=a
n+
(n∈N
*),则S
2014=( )
考点:数列的求和
专题:等差数列与等比数列
分析:由已知条件利用递推思想分别求出a
1,a
2,a
3,由此猜想
an=-,从而能求出S
2014.
解答:解:∵2S
n=a
n+
(n∈N
*),
∴S
n=
(a
n+
),
当n=1时,
a1=(a1+),解得a
1=1,
当n=2时,
a1+a2=(a2+)),解得
a2=-1(a
n>0),
当n=3时,a
1+a
2+a
3=
(a3+)),解得a
3=
-(a
n>0),
猜想:
an=-.
∴S
2014=a
1+a
2+a
3+…+a
2014=1+
-1+
-+…+
-=
.
故选:D.
点评:本题考查数列的前n项和的求法,解题时要认真审题,注意递推思想和裂项求和法的合理运用.
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
数列{a
n}的通项公式a
n=ncos
,其前n项和为S
n,则S
2014=( )
| A、-1006 | B、1007 |
| C、-1008 | D、1009 |
|
查看答案和解析>>
科目:高中数学
来源:
题型:
数列{a
n}的前n项和为S
n,a
1=1,a
n+1=
S
n(n∈N
*),则
=( )
查看答案和解析>>
科目:高中数学
来源:2015届四川省绵阳市高三一诊测试文科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2015届四川省泸州市高三上学期第一次诊断性考试文科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2015届山东省高三第一次诊断性考试理科数学试卷(解析版)
题型:解答题
已知函数 ,其中
,其中 .
.
(1)当 时,求曲线
时,求曲线 在原点处的切线方程;
在原点处的切线方程;
(2)求 的单调区间;
的单调区间;
(3)若 上存在最大值和最小值,求
上存在最大值和最小值,求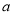 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学
来源:2015届山东省高三第一次诊断性考试理科数学试卷(解析版)
题型:填空题
查看答案和解析>>
科目:高中数学
来源:2015届山东省高三第一次诊断性考试文科数学试卷(解析版)
题型:解答题
查看答案和解析>>
科目:高中数学
来源:2015届山东师范大学附属中学高三第一次模拟考试文科数学试卷(解析版)
题型:解答题
查看答案和解析>>



 出彩同步大试卷系列答案
出彩同步大试卷系列答案 ,其中
,其中 .
. 时,求曲线
时,求曲线 在原点处的切线方程;
在原点处的切线方程; 的单调区间;
的单调区间; 上存在最大值和最小值,求
上存在最大值和最小值,求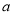 的取值范围.
的取值范围.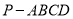 中,底面
中,底面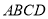 为菱形,
为菱形,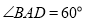 ,
,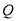 为
为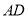 的中点.
的中点.
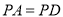 ,求证:平面
,求证:平面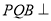 平面
平面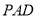 ;
;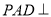 平面
平面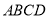 ,且
,且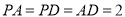 ,点
,点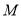 在线段
在线段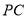 上,且
上,且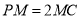 ,求三棱锥
,求三棱锥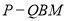 的体积.
的体积.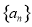 中,已知
中,已知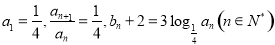 .
.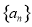 的通项公式;
的通项公式;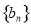 是等差数列;
是等差数列;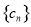 满足
满足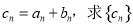 的前
的前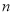 项和
项和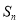 .
.