
如图,在四棱锥中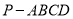 中,底面
中,底面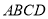 为菱形,
为菱形,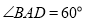 ,
,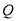 为
为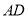 的中点.
的中点.

(1)若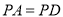 ,求证:平面
,求证:平面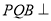 平面
平面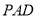 ;
;
(2)若平面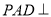 平面
平面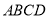 ,且
,且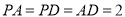 ,点
,点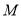 在线段
在线段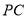 上,且
上,且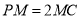 ,求三棱锥
,求三棱锥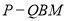 的体积.
的体积.
(1)证明见解析;(2)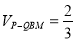
【解析】
试题分析:(1)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键;(2)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.(3)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算.
试题解析:(1)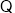
 ,
, 为
为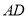 的中点,
的中点, ,又
,又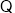 底面
底面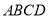 为菱形,
为菱形,
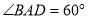 ,
,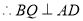 ,又
,又

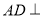 平面
平面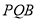 ,又
,又
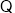
 平面
平面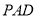 ,
, 平面
平面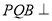 平面
平面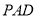
(2)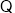 平面
平面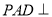 平面
平面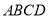 ,平面
,平面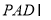 平面
平面 ,
,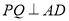
 平面
平面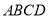 ,
,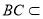 平面
平面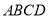 ,
,
 ,又
,又 ,
,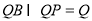 ,
,
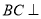 平面
平面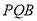 ,又
,又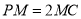 ,
,



考点:1、平面与平面垂直的判断;2、求几何体的体积.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 1 |
| an |
A、2014+
| ||||
B、2014-
| ||||
| C、2014 | ||||
D、
|
查看答案和解析>>
科目:高中数学 来源:2015届四川省泸州市高三上学期第一次诊断性考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分) 设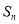 为数列
为数列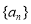 的前
的前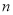 项和,且对任意
项和,且对任意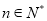 时,点
时,点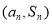 都在函数
都在函数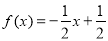 的图象上。
的图象上。
(1)求数列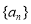 的通项公式;
的通项公式;
(2)设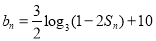 ,求数列
,求数列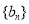 的前
的前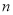 项和
项和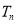 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源:2015届山东省高三第一次诊断性考试理科数学试卷(解析版) 题型:选择题
已知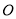 是三角形
是三角形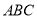 所在平面内一定点,动点
所在平面内一定点,动点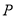 满足
满足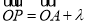 (
( )
)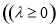 ,则
,则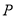 点轨迹一定通过三角形
点轨迹一定通过三角形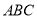 的
的
A.内心 B.外心 C.垂心 D.重心
查看答案和解析>>
科目:高中数学 来源:2015届山东省高三第一次诊断性考试文科数学试卷(解析版) 题型:填空题
观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
照此规律,第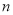 个等式为_______.
个等式为_______.
查看答案和解析>>
科目:高中数学 来源:2015届山东师范大学附属中学高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
已知向量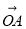 与
与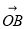 的夹角为
的夹角为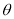 ,
,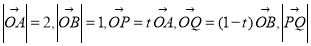
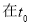 时取得最小值,当
时取得最小值,当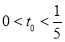 时,夹角
时,夹角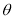 的取值范围为( )
的取值范围为( )
A.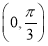 B.
B.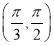 C.
C.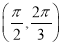 D.
D.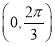
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com