
����С������12�֣�
2012��3��2�գ����һ����������������ġ�����������������.���й涨:�������е�PM2.5��PM2.5��ָ������ֱ��С�ڻ����2.5�Ŀ����Ҳ�ƿ���ο������ƽ��Ũ�Ȳ��ó���35��/�����ף�PM2.5��24Сʱƽ��Ũ�Ȳ��ó���75��/������. ij���л������������ȡ��һ������ȥ��40���PM2.5��24Сʱƽ��Ũ�ȵļ�����ݣ�����ͳ�����£�
|
��� |
PM2.5����/�����ף� |
Ƶ�����죩 |
Ƶ�� |
|
��һ�� |
(0,15] |
4 |
0.1 |
|
�ڶ��� |
(15,30] |
12 |
0.3 |
|
������ |
(30,45] |
8 |
0.2 |
|
������ |
(45,60] |
8 |
0.2 |
|
������ |
(60,75] |
4 |
0.1 |
|
������ |
(75,90) |
4 |
0.1 |
��1��д������������������λ��������д��������̣���
��2�����������ƽ�������������������������˼�룬��PM2.5����ƽ��Ũ�ȿ��ǣ��жϸþ������Ļ����Ƿ���Ҫ�Ľ���˵�����ɣ�
��3����Ƶ����Ϊ���ʣ�����ȥ���ij2�죬����2���иþ�����PM2.5��24Сʱƽ��Ũ�ȷ��ϻ�������������������Ϊ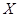 ����
����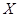 �ķֲ��м���ѧ����
�ķֲ��м���ѧ����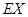 ��
��
��1������Ϊ22.5��/������, ��λ��Ϊ37.5��/�����ף���2���þ������Ļ�����Ҫ�Ľ���
��3������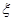 �ķֲ���Ϊ
�ķֲ���Ϊ
|
|
0 |
1 |
2 |
|
|
|
|
|
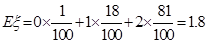 ���죩,��
���죩,��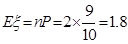 ���죩.
���죩.
��������
�����������1������Ϊ22.5��/������, ��λ��Ϊ37.5��/�����ף� ��������������4��
��2��ȥ��þ�����PM2.5��ƽ��Ũ��Ϊ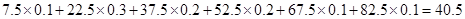 ����/�����ף���
����/�����ף���
��Ϊ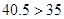 ������ȥ��þ�����PM2.5��ƽ��Ũ�Ȳ����ϻ���������������
������ȥ��þ�����PM2.5��ƽ��Ũ�Ȳ����ϻ���������������
�ʸþ������Ļ�����Ҫ�Ľ��� ��������������������������������8��
��3�����¼�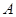 ��ʾ��һ��PM2.5��24Сʱƽ��Ũ�ȷ��ϻ�������������������
��ʾ��һ��PM2.5��24Сʱƽ��Ũ�ȷ��ϻ�������������������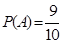 .
.
�������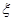 �Ŀ���ȡֵΪ0,1,2.��
�Ŀ���ȡֵΪ0,1,2.�� .����
.����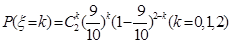 ��
��
���Ա���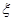 �ķֲ���Ϊ
�ķֲ���Ϊ
|
|
0 |
1 |
2 |
|
|
|
|
|
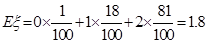 ���죩,��
���죩,��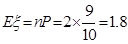 ���죩 ����������12��
���죩 ����������12��
���㣺������Ҫ������ɢ���������������������ֲ���
������ȷ���ֲ��м���ѧ��������������ǹؼ����漰��ϡ��������⣬ע�ʽ����ȷ���ã����е��⡣



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����С������12�֣���֪����![]() ����
����![]() ������
������![]() �����ֵ����Сֵ������
�����ֵ����Сֵ������![]() ���ڶ������ϵĵ�������.
���ڶ������ϵĵ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��2009���Ͼ��ģ�����С������12�֣�
Ϊ��������������ij�о����½�һ���ص㹤�̣��ֱ�Ϊ������ʩ���̡��������̺Ͳ�ҵ���蹤�����࣬�������������Ŀ�ĸ����ֱ�ռ������![]() ��
��![]() ��
��![]() .����3�����˶����ش�����ѡһ����Ŀ���뽨��.��
.����3�����˶����ش�����ѡһ����Ŀ���뽨��.��
��I������ѡ�����Ŀ���������ͬ�ĸ��ʣ� w.w.w.k.s.5.u.c.o.m ![]()
![]()
��II��������1��ѡ�����Ŀ�����������̵ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����С������12�֣�
ij��Ӫ��ҵ����A��B���ֲ�Ʒ�������г������Ԥ�⣬A��Ʒ��������Ͷ�ʳ����ȣ����ϵ��ͼ1��B��Ʒ��������Ͷ�ʵ�����ƽ���������ȣ����ϵ��ͼ2��
��ע��������Ͷ�ʵ�λ����Ԫ��
��1���ֱ�A��B���ֲ�Ʒ�������ʾΪͶ�ʵĺ�������д�����ǵĺ�����ϵʽ.��2������ҵ�ѳO��10��Ԫ�ʽ𣬲�ȫ��Ͷ�뵽A��B���ֲ�Ʒ���������ʣ�����������10��ԪͶ�ʣ�����ʹ��ҵ�������������������Ϊ������Ԫ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com