
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 若有一个正实根,一个负实根,则
若有一个正实根,一个负实根,则 ;
; 是偶函数,但不是奇函数;
是偶函数,但不是奇函数; 的值域是
的值域是 ,则函数
,则函数 的值域为
的值域为 ;
; 和直线
和直线 的公共点个数是
的公共点个数是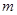 ,则
,则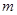 的值不可能是
的值不可能是 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
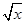 +2)=x+4
+2)=x+4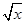 ,求f(x);
,求f(x);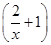 =lgx,求f(x);
=lgx,求f(x);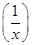 =2x,x∈R且x≠0,求f(x);
=2x,x∈R且x≠0,求f(x);查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 )x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元.
)x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com