练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数f（x）的定义域为R，f（x）= ，且对任意的x∈R都有f（x+1）=﹣ ，若在区间[﹣5，1]上函数g（x）=f（x）﹣mx+m恰有5个不同零点，则实数m的取值范围是（ ）
    A.[﹣ ，﹣ ）
    B.（﹣ ，﹣ ]
    C.（﹣ ，0]
    D.（﹣ ，﹣ ]

    【答案】A
    【解析】解：∵f（x+1）=﹣ ，∴f（x+2）=﹣ ， ∴f（x）=f（x+2），即f（x）的周期为2．
    作出f（x）在[﹣5，1]上的函数图象如图所示：

    令g（x）=0得f（x）=mx﹣m，
    则直线y=mx﹣m与f（x）在[﹣5，1]上有5个交点．
    当直线y=mx﹣m过点（﹣3，1）时，直线y=mx﹣m与f（x）在[﹣5，1]上恰好有5个交点，
    此时﹣3m﹣m=1，即m=﹣ ，
    当直线y=mx﹣m过点（﹣5，1）时，直线y=mx﹣m与f（x）在[﹣5，1]上恰好有6个交点，
    此时﹣5m﹣m=1，即m=﹣ ．
    ∴﹣ ≤m＜﹣ ．
    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|3≤3x≤27}， ．
    （1）分别求A∩B，（RB）∪A；
    （2）已知集合C={x|1＜x＜a}，若CA，求实数a的取值集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=4sinωxsin（ωx+ ）﹣1（ω＞0），f（x）的最小正周期为π． （Ⅰ）当x∈[0， ]时，求f（x）的最大值；
    （Ⅱ）请用“五点作图法”画出f（x）在[0，π]上的图象．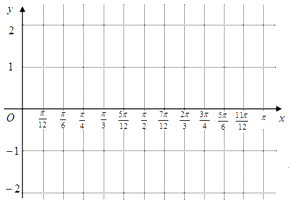

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在边长为4的菱形中，，现沿对角线把折起，折起后使的余弦值为

    （1）求证：平面平面；

    （2）若是的中点，求三棱锥的体积

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现有长分别为1m、2m、3m的钢管各3根（每根钢管质地均匀、粗细相同附有不同的编号），从中随机抽取2根（假设各钢管被抽取的可能性是均等的），再将抽取的钢管相接焊成笔直的一根．若X表示新焊成的钢管的长度（焊接误差不计）．
    （1）求X的分布列；
    （2）若Y=﹣λ2X+λ+1，E（Y）＞1，求实数λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

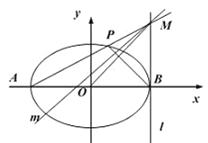
    【题目】如图，在平面直角坐标系中，椭圆的焦距为2，且过点.

    （1）求椭圆的方程；

    （2）若点分别是椭圆的左右顶点，直线经过点且垂直与轴，点是椭圆上异于的任意一点，直线交于点.

    ①设直线的斜率为，直线的斜率为，求证：为定值；

    ②设过点垂直于的直线为 ，求证：直线过定点，并求出定点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数 (为自然对数的底数），.

    （1）证明：当时， 没有零点；

    （2）若当时， 恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C：x2+（y﹣1）2=5，直线l：mx﹣y+1﹣m=0． （Ⅰ）求证：对m∈R，直线l与圆C总有两个不同交点；
    （Ⅱ）设l与圆C交与不同两点A、B，求弦AB的中点M的轨迹方程；
    （Ⅲ）若定点P（1，1）分弦AB为 = ，求此时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}的前n项和为Sn ， 若对任意的正整数n，总存在正整数m，使得Sn=am ， 则称{an}是“H数列”．
    （1）若数列{an}的前n项和为Sn=2n（n∈N*），证明：{an}是“H数列”；
    （2）设{an}是等差数列，其首项a1=1，公差d＜0，若{an}是“H数列”，求d的值；
    （3）证明：对任意的等差数列{an}，总存在两个“H数列”{bn}和{cn}，使得an=bn+cn（n∈N*）成立．

    查看答案和解析>>

    同步练习册答案