
【题目】已知圆 ![]() 与圆
与圆 ![]() :
: ![]() 关于直线
关于直线 ![]() 对称,且点
对称,且点 ![]() 在圆
在圆 ![]() 上.
上.
(1)判断圆 ![]() 与圆
与圆 ![]() 的公切线的条数;
的公切线的条数;
(2)设 ![]() 为圆
为圆 ![]() 上任意一点,
上任意一点, ![]() ,
, ![]() ,
, ![]() 三点不共线,
三点不共线, ![]() 为
为 ![]() 的平分线,且交
的平分线,且交 ![]() 于
于 ![]() ,求证:
,求证: ![]() 与
与 ![]() 的面积之比为定值.
的面积之比为定值.
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D. 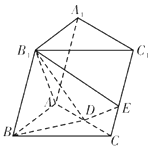
(1)求证:平面ABB1A1⊥平面ABC;
(2)在线段CC1(不含端点)上,是否存在点E,使得二面角E﹣B1D﹣B的余弦值为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有7名学科竞赛优胜者,其中语文学科是A1 , A2 , 数学学科是B1 , B2 , 英语学科是C1 , C2 , 物理学科是D1 , 从竞赛优胜者中选出3名组成一个代表队,要求每个学科至多选出1名.
(1)求B1被选中的概率;
(2)求代表队中有物理优胜者的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于两条平行直线和圆的位置关系定义如下:若两直线中至少有一条与圆相切,则称该位置关系为“平行相切”;若两直线都与圆相离,则称该位置关系为“平行相离”;否则称为“平行相交”.已知直线l1:ax+3y+6=0,l2:2x+(a+1)y+6=0与圆C:x2+y2+2x=b2-1(b>0)的位置关系是“平行相交”,则实数b的取值范围为 ( )
A.( ![]() ,
, ![]() )
)
B.(0, ![]() )
)
C.(0, ![]() )
)
D.( ![]() ,
, ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:k2﹣8k﹣20≤0,命题q:方程 ![]() =1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
=1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
(Ⅱ)若命题“p∨q”为真,命题“p∧q”为假,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an},a1=1,a6=32,Sn是等差数列{bn}的前n项和,b1=3,S5=35.
(1)求数列{an},{bn}的通项公式;
(2)设cn=an+bn , 求数列{cn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com