
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 是菱形,
是菱形,![]() ⊥平面
⊥平面![]() 且
且![]() .
.

(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)若![]() 设
设![]() 与平面
与平面![]() 所成夹角为
所成夹角为![]() ,且
,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
分析:(1)根据已知可得![]() 和
和![]() ,由线面垂直判定定理可证
,由线面垂直判定定理可证![]() 平面
平面![]() ,再由面面垂直判定定理证得平面
,再由面面垂直判定定理证得平面![]() ⊥平面
⊥平面![]() .
.
(2)解法一:向量法,设![]() ,以
,以![]() 为原点,作
为原点,作![]() ,以
,以![]() 的方向分别为
的方向分别为![]() 轴,
轴,![]() 轴的正方向,建空间直角坐标系,求得
轴的正方向,建空间直角坐标系,求得![]() 的坐标,运用向量的坐标表示和向量的垂直条件,求得平面
的坐标,运用向量的坐标表示和向量的垂直条件,求得平面![]() 和平面
和平面![]() 的的法向量,再由向量的夹角公式,计算即可得到所求的值.
的的法向量,再由向量的夹角公式,计算即可得到所求的值.
解法二:三垂线法,连接AC交BD于O,连接EO、FO,过点F做FM⊥EC于M,连OM,由已知可以证明FO⊥面AEC,∠FMO即为二面角A-EC-F的平面角,通过菱形的性质、勾股定理和等面积法求得cos∠FMO,得到答案.
解法三:射影面积法,连接AC交BD于O,连接EO、FO,根据已知条件计算![]() ,
,![]() ,二面角的余弦值cosθ=
,二面角的余弦值cosθ=![]() ,即可求得答案.
,即可求得答案.
详解:(1)证明:连结![]()
![]() 四边形
四边形![]() 是菱形,
是菱形,![]() ,
,
![]() ⊥平面
⊥平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ⊥平面
⊥平面![]() .
.
(2)解:解法一:设 ![]() ,
,
![]() 四边形
四边形![]() 是菱形,
是菱形,![]() ,
,
![]() 、
、![]() 为等边三角形,
为等边三角形,![]()
![]() ,
,
![]()
![]() 是
是![]() 的中点,
的中点, ![]()
![]() ,
,
![]()
![]() ⊥平面
⊥平面![]() ,
,![]() ,
,
![]() 在
在![]() 中有,
中有,![]() ,
,![]() ,
,
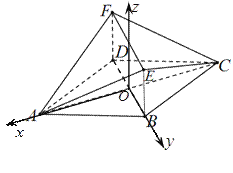
以![]() 为原点,作
为原点,作![]() ,以
,以![]() 的方向分别为
的方向分别为![]() 轴,
轴,![]() 轴的正方向,建空间直角坐标系
轴的正方向,建空间直角坐标系![]() 如图所示,则
如图所示,则![]()
所以![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
由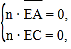 得
得![]() 设
设![]() ,解得
,解得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由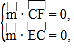 得
得![]() 设
设![]() ,解得
,解得![]() .
.
设二面角![]() 的为
的为![]() ,则
,则![]()
结合图可知,二面角![]() 的余弦值为
的余弦值为![]() .
.
解法二:
∵EB⊥面ABCD,
∴∠EAB即为EA与平面ABCD所成的角
在Rt△EAB中,cos∠EAB=![]() 又AB=2,∴AE=
又AB=2,∴AE=![]()
∴EB=DF=1
连接AC交BD于O,连接EO、FO
菱形ABCD中,∠BAD=60°,∴BD=AB=2
矩形BEFD中,FO=EO=![]() ,EF=2,EO+FO=EF,∴FO⊥EO
,EF=2,EO+FO=EF,∴FO⊥EO
又AC⊥面BEFD, FO面BEFD,∴FO⊥AC,
AC∩EO=O,AC、EO面AEC,∴FO⊥面AEC
又EC面AEC,∴FO⊥EC
过点F做FM⊥EC于M,连OM,
又FO⊥EC, FM∩FO=F, FM、FO面FMO,∴EC⊥面FMO
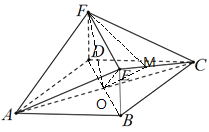
OM面FMO,∴EC⊥MO
∴∠FMO即为二面角A-EC-F的平面角
AC⊥面BEFD, EO面BEFD,∴AC⊥EO
又O为AC的中点,∴EC=AE=![]()
Rt△OEC中,OC=![]() , EC=
, EC=![]() ,∴OE=
,∴OE=![]() ,∴OM =
,∴OM =![]()
Rt△OFM中,OF=![]() , OM =
, OM =![]() ,∴FM =
,∴FM =![]()
∴cos∠FMO=![]()
即二面角A-EC-F的余弦值为![]()
解法三:
连接AC交BD于O,连接EO、FO
菱形ABCD中,∠BAD=60°,∴BD=AB=2
矩形BEFD中,FO=EO=![]() ,EF=2,EO+FO=EF,∴FO⊥EO
,EF=2,EO+FO=EF,∴FO⊥EO
又AC⊥面BEFD, FO面BEFD,∴FO⊥AC,
AC∩EO=O,AC、EO面AEC,∴FO⊥面AEC
又∵EB⊥面ABCD,
∴∠EAB即为EA与平面ABCD所成的角
在Rt△EAB中,cos∠EAB=![]() 又AB=2,∴AE=
又AB=2,∴AE=![]()
∴EB=DF=1
在Rt△EBC、Rt△FDC中可得FC=EC=![]()
在△EFC中,FC=EC=![]() ,EF=2,∴
,EF=2,∴![]()
在△AEC中, AE=EC=![]() ,O为AC中点,∴OE⊥OC
,O为AC中点,∴OE⊥OC
在Rt△OEC,OE=![]() , OC=
, OC=![]() ,∴
,∴![]()
设△EFC、△OEC在EC边上的高分别为h、m,
二面角A-EC-F的平面角设为θ,
则cosθ=![]()
即二面角A-EC-F的余弦值为![]() .
.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)射线![]() 的极坐标方程为
的极坐标方程为![]() ,若射线
,若射线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的一个顶点为![]() ,焦点在x轴上,若椭圆的右焦点到直线
,焦点在x轴上,若椭圆的右焦点到直线![]() 的距离是3.
的距离是3.
![]() 求椭圆E的方程;
求椭圆E的方程;
![]() 设过点A的直线l与该椭圆交于另一点B,当弦AB的长度最大时,求直线l的方程.
设过点A的直线l与该椭圆交于另一点B,当弦AB的长度最大时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是![]() (
(![]() ≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是
≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是![]() .若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是
.若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是

A. 165 cmB. 175 cmC. 185 cmD. 190cm
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 过点
过点![]() 且渐近线为
且渐近线为![]() ,则下列结论正确的个数为( )
,则下列结论正确的个数为( )
①![]() 的实轴长为
的实轴长为![]() ;②
;②![]() 的离心率为
的离心率为![]() ;
;
③曲线![]() 经过
经过![]() 的一个焦点;④直线
的一个焦点;④直线![]() 与
与![]() 有两个公共点.
有两个公共点.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得![]() 分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得
分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得![]() 分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
(1)求![]() 的分布列;
的分布列;
(2)若甲药、乙药在试验开始时都赋予4分,![]() 表示“甲药的累计得分为
表示“甲药的累计得分为![]() 时,最终认为甲药比乙药更有效”的概率,则
时,最终认为甲药比乙药更有效”的概率,则![]() ,
,![]() ,
,![]()
![]() ,其中
,其中![]() ,
,![]() ,
,![]() .假设
.假设![]() ,
,![]() .
.
(i)证明:![]()
![]() 为等比数列;
为等比数列;
(ii)求![]() ,并根据
,并根据![]() 的值解释这种试验方案的合理性.
的值解释这种试验方案的合理性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]() 经过点
经过点![]() ,两条渐近线的夹角为
,两条渐近线的夹角为![]() ,直线
,直线![]() 交双曲线于
交双曲线于![]() 、
、![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若![]() 过原点,
过原点,![]() 为双曲线上异于
为双曲线上异于![]() 、
、![]() 的一点,且直线
的一点,且直线![]() 、
、![]() 的斜率为
的斜率为![]() 、
、![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)若![]() 过双曲线的右焦点
过双曲线的右焦点![]() ,是否存在
,是否存在![]() 轴上的点
轴上的点![]() ,使得直线
,使得直线![]() 绕点
绕点![]() 无论怎样转动,都有
无论怎样转动,都有![]() 成立?若存在,求出
成立?若存在,求出![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是由矩形![]() 和菱形
和菱形![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
, ![]() ,将其沿
,将其沿![]() 折起使得
折起使得![]() 与
与![]() 重合,连结
重合,连结![]() ,如图2.
,如图2.
(1)证明图2中的![]() 四点共面,且平面
四点共面,且平面![]() 平面
平面![]() ;
;
(2)求图2中的四边形![]() 的面积.
的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com