
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() 为函数
为函数![]() 的极小值点,求
的极小值点,求![]() 的取值范围,并求
的取值范围,并求![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ,
,![]() 的递减区间
的递减区间![]() 和
和![]() ,递增区间为
,递增区间为![]() ,(Ⅱ)
,(Ⅱ)![]()
【解析】
(Ⅰ)首先求出函数![]() 导数,分类讨论
导数,分类讨论![]() 或
或![]() ,判断
,判断![]() 的正负即可求解.
的正负即可求解.
(Ⅱ)令![]() ,且
,且![]() ,求出
,求出![]() ,令
,令![]() ,且
,且![]() ,求出
,求出![]() 在
在![]() 上单调递增,进而分类讨论
上单调递增,进而分类讨论![]() 或
或![]() ,求出
,求出![]() 的单调区间,即可求出
的单调区间,即可求出![]() 的单调区间,判断
的单调区间,判断![]() 的正负即可求解.
的正负即可求解.
(Ⅰ)由题意知:![]() ,且
,且![]() ,
,
若![]() ,即
,即![]() 时,当
时,当![]() ,
,![]() ,所以
,所以![]() 不可能为
不可能为![]() 的极小值点;
的极小值点;
若![]() ,即
,即![]() 时,令
时,令![]() ;
;
令![]() 或
或![]() ,
,
所以![]() 的递减区间
的递减区间![]() 和
和![]() ,递增区间为
,递增区间为![]() ,
,
所以![]() 为函数
为函数![]() 的极小值点,
的极小值点,
综上:![]() ,
,![]() 的递减区间
的递减区间![]() 和
和![]() ,递增区间为
,递增区间为![]() .
.
(Ⅱ)令![]() ,
,
则![]() ,
,
![]() ,
,
令![]() ,则
,则![]() ,
,
因为![]() ,令
,令![]() ,
,
则![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
(1)当![]() ,即
,即![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 对
对![]() 恒成立.
恒成立.
所以![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,![]() ,符合题意;
,符合题意;
(2)当![]() ,即
,即![]() 时,因为
时,因为![]() ,
,
又![]() 且
且![]() ,
,
又![]() 在
在![]() 上连续且单调递增,所以存在
上连续且单调递增,所以存在![]() ,使得
,使得![]() ,此时,当
,此时,当![]() 时,
时,![]() ,所以
,所以![]() 单调递减,所以
单调递减,所以![]() ,
,
所以![]() ,所以
,所以![]() 在
在![]() 单调递减,
单调递减,
所以![]() ,
,![]() ,矛盾,舍去.
,矛盾,舍去.
综上:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知![]() 为定义在
为定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,有
时,有![]() ,且当
,且当![]() 时,
时,![]() ,下列命题正确的是( )
,下列命题正确的是( )
A.![]() B.函数
B.函数![]() 在定义域上是周期为
在定义域上是周期为![]() 的函数
的函数
C.直线![]() 与函数
与函数![]() 的图象有
的图象有![]() 个交点D.函数
个交点D.函数![]() 的值域为
的值域为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省在2017年启动了“3+3”高考模式.所谓“3+3”高考模式,就是语文、数学、外语(简称语、数、外)为高考必考科目,从物理、化学、生物、政治、历史、地理(简称理、化、生、政、史、地)六门学科中任选三门作为选考科目.该省某中学2017级高一新生共有990人,学籍号的末四位数从0001到0990.
(1)现从高一学生中抽样调查110名学生的选考情况,问:采用什么样的抽样方法较为恰当?(只写出结论,不需要说明理由)
(2)据某教育机构统计,学生所选三门学科在将来报考专业时受限制的百分比是不同的.该机构统计了受限百分比较小的十二种选择的百分比值![]() ,制作出如下条形图.
,制作出如下条形图.
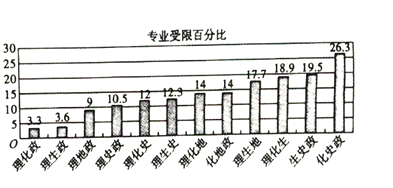
设以上条形图中受限百分比的均值为![]() ,标准差为
,标准差为![]() .如果一个学生所选三门学科专业受限百分比在区间
.如果一个学生所选三门学科专业受限百分比在区间![]() 内,我们称该选择为“恰当选择”.该校李明同学选择了化学,然后从余下五门选考科目中任选两门.问李明的选择为“恰当选择"的概率是多少?(均值
内,我们称该选择为“恰当选择”.该校李明同学选择了化学,然后从余下五门选考科目中任选两门.问李明的选择为“恰当选择"的概率是多少?(均值![]() ,标准差
,标准差![]() 均精确到0.1)
均精确到0.1)
(参考公式和数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() ,
,![]() 是曲线段
是曲线段![]() :
:![]() (
(![]() 是参数,
是参数,![]() )的左、右端点,
)的左、右端点,![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的动点,过点
的动点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
(1)建立适当的极坐标系,写出点![]() 轨迹的极坐标方程;
轨迹的极坐标方程;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为![]() .
.
(1)问该厂至少有多少名维修工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不小于![]() ?
?
(2)已知1名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,能使该厂产生5万元的利润,否则将不产生利润.若该厂现有2名工人,求该厂每月获利的均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com