练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．在三棱锥A-BCD中，E，F，G分别是AB，AC，BD的中点，若AD与BC所成的角是60°，那么∠FEG为（　　）
    A．60°B．30°C．120°D．60°或120°

    分析 如果D对ABC的投影在ABC内，∠FEG等于AD与BC所成的角；如果D对ABC的投影在ABC外，∠FEG等于AD与BC所成的角的补角．

    解答 解：如图一，D对ABC的投影在ABC内，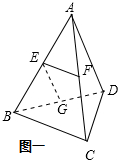
    连接EF、EG，
    ∵E，F，G分别是AB，AC，BD的中点，
    ∴EF∥BC，EG∥AD，
    又AD与BC所成的角是60°，
    ∴∠FEG=60°．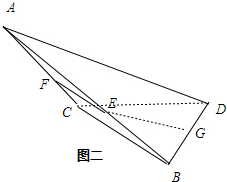
    如图二，D对ABC的投影在ABC外，
    连接EF、EG，
    ∵E，F，G分别是AB，AC，BD的中点，
    ∴EF∥BC，EG∥AD，
    又AD与BC所成的角是60°，
    ∴∠FEG=180°-60°=120°．
    故∠FEG为60°或120°．
    故选：D．

    点评 本题考查异面直线所成角的大小的求法，是中档题，解题时要认真审题，易错点是容易丢失D对ABC的投影在ABC外的解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．设命题p：“?x＞1，x2≥x，则其否定非p为（　　）
    A．?x＞1，x2≤xB．$?{x}_{0}＞1，{x}_{0}^{2}＞{x}_{0}$
    C．$?{x}_{0}≤1，{x}_{0}^{2}≤{x}_{0}$D．$?{x}_{0}＞1，{x}_{0}^{2}＜{x}_{0}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知△ABC三点A（-3，4），B（1，2），C（5，-2）．求该三角形三条中线所在直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．有一个正六棱锥（底面为正六边形，侧面为全等的等腰三角形的棱锥），底面边长为3cm，高为3cm，画出这个正六棱锥的直观图．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知命题A是C的充分条件，B是C的充要条件，B是D的必要条件，试问命题A是B的什么条件，D是C的什么条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．在△ABC中，角A，B，C所对的边为a，b，c，已知a=2c，且A-C=$\frac{π}{2}$．
    （1）求cosC的值；
    （2）当b=1时，求c．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数f（x）=x2+4x+2，g（x）=2ex（x+1），若x≥-2时，f（x）≤kg（x），求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知命题p：关于x的方程log2（ax2-2x+2）=2在[1，2]内有解；命题q：函数f（x）=m（x2-1）+x-a的图象与x轴有交点．
    （1）若p是真命题．求实数a的取值范围；
    （2）若￢p是￢q的必要不充分条件，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．若不等式x+lnx≤kx+b≤x2对?x∈（0，+∞）恒成立，则k+3b的值-1．

    查看答案和解析>>

    同步练习册答案