在等比数列{an}中,前n项和为Sn,若Sm,Sm+2,Sm+1成等差数列,则am,am+2,am+1成等差数列.
(1)写出这个命题的逆命题;
(2)判断逆命题是否为真?并给出证明.
【答案】
分析:(1)根据逆命题的要求直接写出逆命题即可.
(2)根据逆命题的条件推出公比q的值,然后验证结论是否成立.
解答:解:(1)在等比数列{a
n}中,前n项和为S
n,若a
m,a
m+2,a
m+1成等差数列,则S
m,S
m+2,S
m+1成等差数列.
(2)数列{a
n}的首项为a
1,公比为q.由题意知:2a
m+2=a
m+a
m+1即2•a
1•q
m+1=a
1•q
m-1+a
1•q
m∵a
1≠0,q≠0,∴2q
2-q-1=0,∴
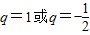
当q=1时,有S
m=ma
1,S
m+2=(m+2)a
1,S
m+1=(m+1)a
1,
显然:2S
m+2≠S
m+S
m+1.此时逆命题为假.
当

时,有
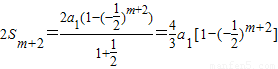
,

∴2S
m+2=S
m+S
m+1,此时逆命题为真.
点评:本题是中档题,考查数列的基本知识,命题与逆命题的关系,考查计算能力,常考题型.

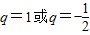
 时,有
时,有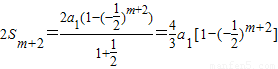 ,
,

