
【题目】在直角坐标系中,已知椭圆![]() 经过点
经过点![]() ,且其左右焦点的坐标分别是
,且其左右焦点的坐标分别是![]() ,
,![]() .
.
(1)求椭圆![]() 的离心率及标准方程;
的离心率及标准方程;
(2)设![]() 为动点,其中
为动点,其中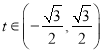 ,直线
,直线![]() 经过点
经过点![]() 且与椭圆
且与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() 为
为![]() 的中点,是否存在定点
的中点,是否存在定点![]() ,使
,使![]() 恒成立?若存在,求点
恒成立?若存在,求点![]() 的坐标;若不存在,说明理由
的坐标;若不存在,说明理由
科目:高中数学 来源: 题型:
【题目】(2018·湖南师大附中摸底)已知直线l经过点P(-4,-3),且被圆(x+1)2+(y+2)2=25截得的弦长为8,则直线l的方程是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的焦点为
的焦点为![]() ,椭圆
,椭圆![]() 的中心在原点,
的中心在原点,![]() 为其右焦点,点
为其右焦点,点![]() 为曲线
为曲线![]() 和
和![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为抛物线
为抛物线![]() 上的两个动点,且使得线段
上的两个动点,且使得线段![]() 的中点
的中点![]() 在直线
在直线![]() 上,
上,
![]() 为定点,求
为定点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】前段时间,某机构调查人们对屯商平台“618”活动的认可度(分为:强烈和一般两类),随机抽取了100人统计得到2×2列联表的部分数据如表:
一般 | 强烈 | 合计 | |
男 | 45 | ||
女 | 10 | ||
合计 | 75 | 100 |
(1)补全2×2列联表中的数据;
(2)判断能否有95%的把握认为人们的认可度是否为“强烈”与性别有关?
参考公式及数据: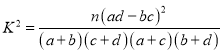
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式![]() 确定的平面区域为U,
确定的平面区域为U,![]() 确定的平面区域为V.
确定的平面区域为V.
(1)定义横、纵坐标为整数的点为“整点”,在区域U内任取3个整点,求这些整点中恰有2个整点在区域V内的概率;
(2)设集合![]() ;集合
;集合![]() 若从集合A到集合B可以建立m个不同的映射?从集合B到集合A可以建立n个不同的映射,求m,n的值.
若从集合A到集合B可以建立m个不同的映射?从集合B到集合A可以建立n个不同的映射,求m,n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为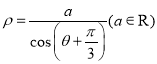 ,直线
,直线![]() 经过椭圆
经过椭圆![]() 的右焦点
的右焦点![]() .
.
(1)求实数![]() 的值;
的值;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com