
【题目】对于任意实数![]() ,定义
,定义![]() 设函数
设函数![]() ,
,![]() ,则函数
,则函数![]() 的最大值是________.
的最大值是________.
【答案】1
【解析】
分别作出函数f(x)=﹣3+x和g(x)=log2x的图象,结合函数f(x)=﹣3+x和g(x)=log2x的图象可知,在这两个函数的交点处函数h(x)=min{f(x),g(x)}的最大值.
∵x>0,∴f(x)=﹣x+3<3,g(x)=log2x∈R,分别作出函数f(x)=﹣3+x和g(x)=log2x
的图象,结合函数f(x)=﹣3+x和g(x)=log2x的图象可知,
h(x)=min{f(x),g(x)}的图象,
在这两个函数的交点处函数h(x)=min{f(x),g(x)}的最大值.
解方程组![]() 得
得![]() ,
,
∴函数h(x)=min{f(x),g(x)}的最大值是1.
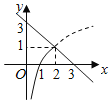
故答案为:1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某食品厂为了检查一条自动包装流水线的生产情况,随即抽取该流水线上![]() 件产品作为样本算出他们的重量(单位:克)重量的分组区间为
件产品作为样本算出他们的重量(单位:克)重量的分组区间为![]() ,
,![]() ,……
,……![]() ,由此得到样本的频率分布直方图,如图所示.
,由此得到样本的频率分布直方图,如图所示.
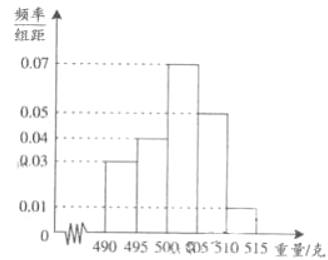
(1)根据频率分布直方图,求重量超过![]() 克的产品数量.
克的产品数量.
(2)在上述抽取的![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为重量超过
为重量超过![]() 克的产品数量,求
克的产品数量,求![]() 的分布列.
的分布列.
(3)从流水线上任取![]() 件产品,求恰有
件产品,求恰有![]() 件产品合格的重量超过
件产品合格的重量超过![]() 克的概率.
克的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,不过原点的直线
,不过原点的直线![]() 与椭圆交于A、B两点.
与椭圆交于A、B两点.
(1)求![]() 面积的最大值.
面积的最大值.
(2)是否存在椭圆![]() ,使得对于椭圆
,使得对于椭圆![]() 的每一条切线与椭圆
的每一条切线与椭圆![]() 均相交,设交于A、B两点,且
均相交,设交于A、B两点,且![]() 恰取最大值?若存在,求出该椭圆;若不存在,说明理由.
恰取最大值?若存在,求出该椭圆;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
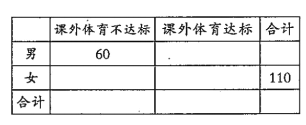
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集的数据分成![]() 六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
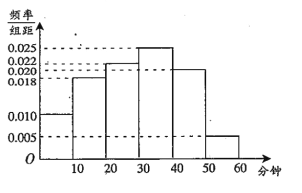
(1)请根据直方图中的数据填写下面的![]() 列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
(2)现按照“课外体育达标”与“课外体育不达标”进行分层抽样,抽取8人,再从这8名学生中随机抽取3人参加体育知识问卷调查,记“课外体育不达标”的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com