
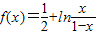 .
.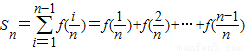 ,其中n∈N*且n≥2,求S2011;
,其中n∈N*且n≥2,求S2011;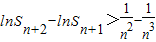 .
. .
. ,
, ,
, .
. ,使得函数f(x)的图象上任意一点P关于M点对称的点Q也在函数f(x)的图象上.
,使得函数f(x)的图象上任意一点P关于M点对称的点Q也在函数f(x)的图象上. …①
…① …②
…② ,
, ,
, 等价于
等价于 .…(10分)
.…(10分) ,
, ,
, 成立.…(14分)
成立.…(14分)

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源:2012-2013学年宁夏高三第五次月考理科数学试卷(解析版) 题型:解答题
(本小题满分l0分)选修4—5:不等式选讲
已知函数 .
.
(1)求证: ;
;
(2)解不等式 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市高三上学期10月月考数学卷 题型:解答题
(本题满分15分)已知函数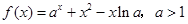 .
.
(I)求证: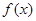 在
在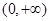 上单调递增;
上单调递增;
(Ⅱ)函数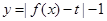 有三个零点,求
有三个零点,求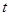 值;
值;
(Ⅲ)对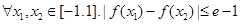 恒成立,求
恒成立,求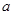 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com