
【题目】已知函数![]() ,
,![]() 的导函数为
的导函数为![]() .
.
(1)试讨论函数![]() 的零点个数;
的零点个数;
(2)若对任意的![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)先求函数的定义域,然后求函数的导数![]() ,对
,对![]() 分类讨论,将
分类讨论,将![]() 的零点问题,转化为直线
的零点问题,转化为直线![]() 与函数
与函数![]() 图象的交点个数来求解出来.(2)构造函数
图象的交点个数来求解出来.(2)构造函数![]() ,将原问题转化为
,将原问题转化为![]() 对
对![]() 恒成立,先利用
恒成立,先利用![]() 确定
确定![]() 的一个范围,然后利用
的一个范围,然后利用![]() 的二阶导数验证在这个范围内,
的二阶导数验证在这个范围内,![]() 的最大值不大于零,由此求得
的最大值不大于零,由此求得![]() 的取值范围.
的取值范围.
解:(1)由题意得![]() 的定义域为
的定义域为![]() ,
,![]() .
.
(i)当![]() 时,
时,![]() ,此时没有零点;
,此时没有零点;
(ii)当![]() 时,
时,![]() ,
,
![]() 的零点个数等于直线
的零点个数等于直线![]() 与函数
与函数![]() 图象的交点个数,可知直线
图象的交点个数,可知直线![]() 与函数
与函数![]() 图象的相切点
图象的相切点![]() ,此时切线的斜率为
,此时切线的斜率为![]() .
.
①当![]() ,即
,即![]() 时,两个图象没有交点,即函数
时,两个图象没有交点,即函数![]() 没有零点;
没有零点;
②当![]() ,即
,即![]() 时,两个图象有两个交点,即函数
时,两个图象有两个交点,即函数![]() 有两个零点;
有两个零点;
③当![]() ,即
,即![]() 时两个图象有一个交点,即函数
时两个图象有一个交点,即函数![]() 有一个零点;
有一个零点;
④当![]() ,即
,即![]() 时,两个图象有一个交点,即函数
时,两个图象有一个交点,即函数![]() 有一个零点.
有一个零点.
综上,当![]() 时,函数
时,函数![]() 没有零点;
没有零点;
当![]() 或
或![]() 时,
时,![]() 有一个零点;
有一个零点;
当![]() 时,
时,![]() 有两个零点.
有两个零点.
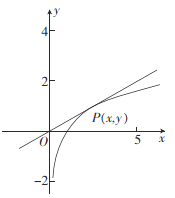
(2)设![]()
![]() ,
,
要使原不等式恒成立,则只要![]() 对
对![]() 恒成立,
恒成立,
所以![]() .
.
令![]() ,则
,则![]() .
.
由于“![]() 对
对![]() 恒成立”的一个必要条件是
恒成立”的一个必要条件是![]() ,即
,即![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递减.
上单调递减.
所以![]() ,
,![]() ,从而
,从而![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,
,![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的动点(点
上的动点(点![]() 与
与![]() 不重合),则下列结论正确的是__________
不重合),则下列结论正确的是__________
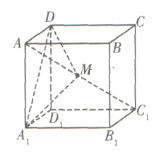
①存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
③![]() 的面积可能等于
的面积可能等于![]() ;
;
④若![]() 分别是
分别是![]() 在平面
在平面![]() 与平面
与平面![]() 的正投影的面积,则存在点
的正投影的面积,则存在点![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 上的动点
上的动点![]() 到点
到点![]() 的距离减去
的距离减去![]() 到直线
到直线![]() 的距离等于1.
的距离等于1.
(1)求曲线![]() 的方程;
的方程;
(2)若直线 ![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求证:直线
两点,求证:直线![]() 与直线
与直线![]() 的倾斜角互补.
的倾斜角互补.
查看答案和解析>>
科目:高中数学 来源: 题型:
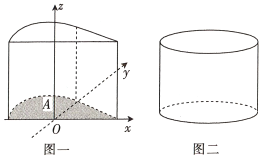
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.该原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图,在空间直角坐标系中的![]() 平面内,若函数
平面内,若函数![]() 的图象与
的图象与![]() 轴围成一个封闭的区域
轴围成一个封闭的区域![]() ,将区域
,将区域![]() 沿
沿![]() 轴的正方向平移8个单位长度,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域
轴的正方向平移8个单位长度,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域![]() 的面积相等,则此圆柱的体积为__________.
的面积相等,则此圆柱的体积为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据说伟大的阿基米德逝世后,敌军将领马塞拉斯给他建了一块墓碑,在墓碑上刻了一个如图所示的图案,图案中球的直径、圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面.
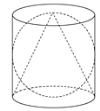
(1)试计算出图案中球与圆柱的体积比;
(2)假设球半径![]() .试计算出图案中圆锥的体积和表面积.
.试计算出图案中圆锥的体积和表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,左焦点
的中心在原点,左焦点![]() 、右焦点
、右焦点![]() 都在
都在![]() 轴上,点
轴上,点![]() 是椭圆
是椭圆![]() 上的动点,
上的动点,![]() 的面积的最大值为
的面积的最大值为![]() ,在
,在![]() 轴上方使
轴上方使![]() 成立的点
成立的点![]() 只有一个.
只有一个.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的两直线
的两直线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于点
交于点![]() ,
,![]() 和点
和点![]() ,
,![]() ,且
,且![]() ,比较
,比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2ax-![]() x2-3ln x,其中a∈R,为常数.
x2-3ln x,其中a∈R,为常数.
(1)若f(x)在x∈[1,+∞)上是减函数,求实数a的取值范围;
(2)若x=3是f(x)的极值点,求f(x)在x∈[1,a]上的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com