
【题目】在棱长为1的正方体![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的动点(点
上的动点(点![]() 与
与![]() 不重合),则下列结论正确的是__________
不重合),则下列结论正确的是__________
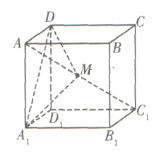
①存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
③![]() 的面积可能等于
的面积可能等于![]() ;
;
④若![]() 分别是
分别是![]() 在平面
在平面![]() 与平面
与平面![]() 的正投影的面积,则存在点
的正投影的面积,则存在点![]() ,使得
,使得![]()
【答案】①②③④
【解析】
根据正方体的结构特征,利用线面位置关系的判定定理和性质定理,以及三角形的面积公式和投影的定义,即可求解,得到答案.
①如图所示,当![]() 是
是![]() 中点时,可知
中点时,可知![]() 也是
也是![]() 中点且
中点且![]() ,
,![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,同理可知
,同理可知![]() ,
,
且![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,故正确;
,故正确;

②如图所示,取![]() 靠近
靠近![]() 的一个三等分点记为
的一个三等分点记为![]() ,记
,记![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() 为
为![]() 靠近
靠近![]() 的一个三等分点,
的一个三等分点,
则![]() 为
为![]() 中点,又
中点,又![]() 为
为![]() 中点,所以
中点,所以![]() ,且
,且![]() ,
,![]() ,
,![]() ,所以平面
,所以平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,故正确;
,故正确;
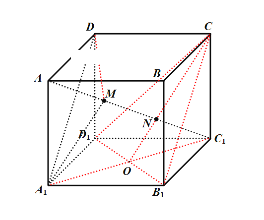
③如图所示,作![]() ,在
,在![]() 中根据等面积得:
中根据等面积得:![]() ,
,
根据对称性可知:![]() ,又
,又![]() ,所以
,所以![]() 是等腰三角形,
是等腰三角形,
则 ,故正确;
,故正确;

④如图所示,设![]() ,
,![]() 在平面
在平面![]() 内的正投影为
内的正投影为![]() ,
,![]() 在平面
在平面![]() 内的正投影为
内的正投影为![]() ,所以
,所以![]() ,
,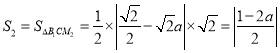 ,当
,当![]() 时,解得:
时,解得:![]() ,故正确.
,故正确.

故答案为 ①②③④



 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】现有一长为100码,宽为80码,球门宽为8码的矩形足球运动场地,如图所示,其中![]() 是足球场地边线所在的直线,球门
是足球场地边线所在的直线,球门![]() 处于所在直线的正中间位置,足球运动员(将其看做点
处于所在直线的正中间位置,足球运动员(将其看做点![]() )在运动场上观察球门的角
)在运动场上观察球门的角![]() 称为视角.
称为视角.
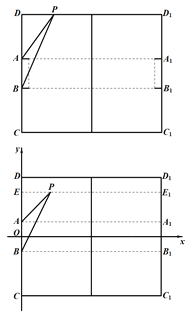
(1)当运动员带球沿着边线![]() 奔跑时,设
奔跑时,设![]() 到底线的距离为
到底线的距离为![]() 码,试求当
码,试求当![]() 为何值时
为何值时![]() 最大;
最大;
(2)理论研究和实践经验表明:张角![]() 越大,射门命中率就越大.现假定运动员在球场都是沿着垂直于底线的方向向底线运球,运动到视角最大的位置即为最佳射门点,以
越大,射门命中率就越大.现假定运动员在球场都是沿着垂直于底线的方向向底线运球,运动到视角最大的位置即为最佳射门点,以![]() 的中点为原点建立如图所示的直角坐标系,求在球场区域
的中点为原点建立如图所示的直角坐标系,求在球场区域![]() 内射门到球门
内射门到球门![]() 的最佳射门点的轨迹.
的最佳射门点的轨迹.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
![]() 根据表中数据,问是否有
根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
![]() 已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了纪念“一带一路”倡议提出五周年,某城市举办了一场知识竞赛,为了了解市民对“一带一路”知识的掌握情况,从回收的有效答卷中按青年组和老年组各随机抽取了40份答卷,发现成绩都在![]() 内,现将成绩按区间
内,现将成绩按区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,绘制成如下的频率分布直方图.
进行分组,绘制成如下的频率分布直方图.
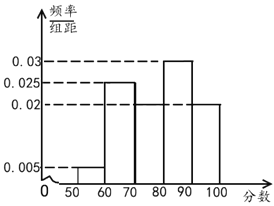
青年组

中老年组
(1)利用直方图估计青年组的中位数和老年组的平均数;
(2)从青年组![]() ,
,![]() 的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自
的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了纪念“一带一路”倡议提出五周年,某城市举办了一场知识竞赛,为了了解市民对“一带一路”知识的掌握情况,从回收的有效答卷中按青年组和老年组各随机抽取了40份答卷,发现成绩都在![]() 内,现将成绩按区间
内,现将成绩按区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,绘制成如下的频率分布直方图.
进行分组,绘制成如下的频率分布直方图.

青年组

中老年组
(1)利用直方图估计青年组的中位数和老年组的平均数;
(2)从青年组![]() ,
,![]() 的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自
的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com